Disjoint Sets
by Eddie HuangOverview
Disjoint sets allows you to organize elements in sets and be able to query which set an element belongs to in essentially constant time.
The data structure to represent disjoint sets is a forest of trees, where each set is represented by a tree and each tree is identified by its root node. Therefore, we call the root node of a tree, the representative of its set.
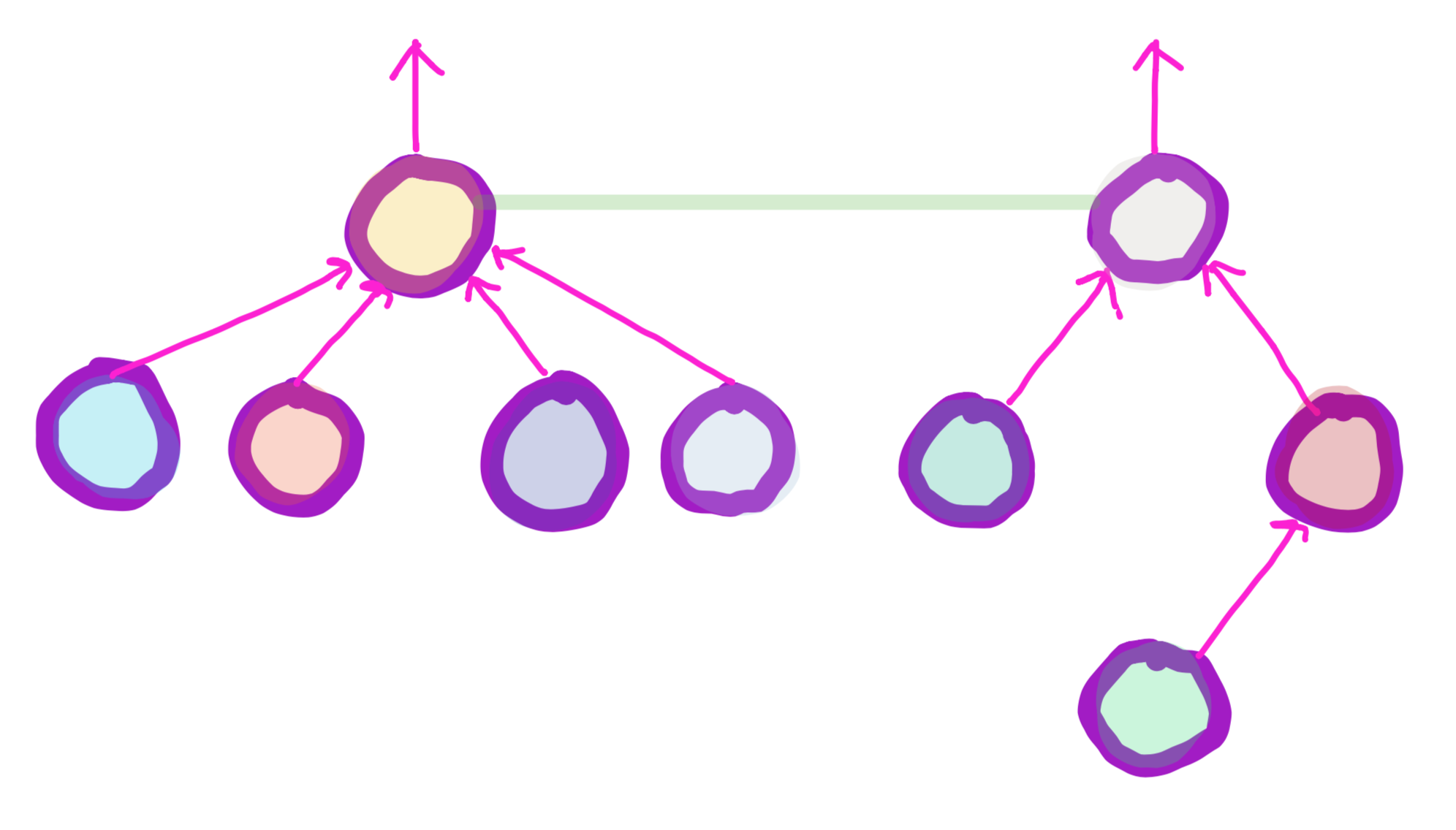
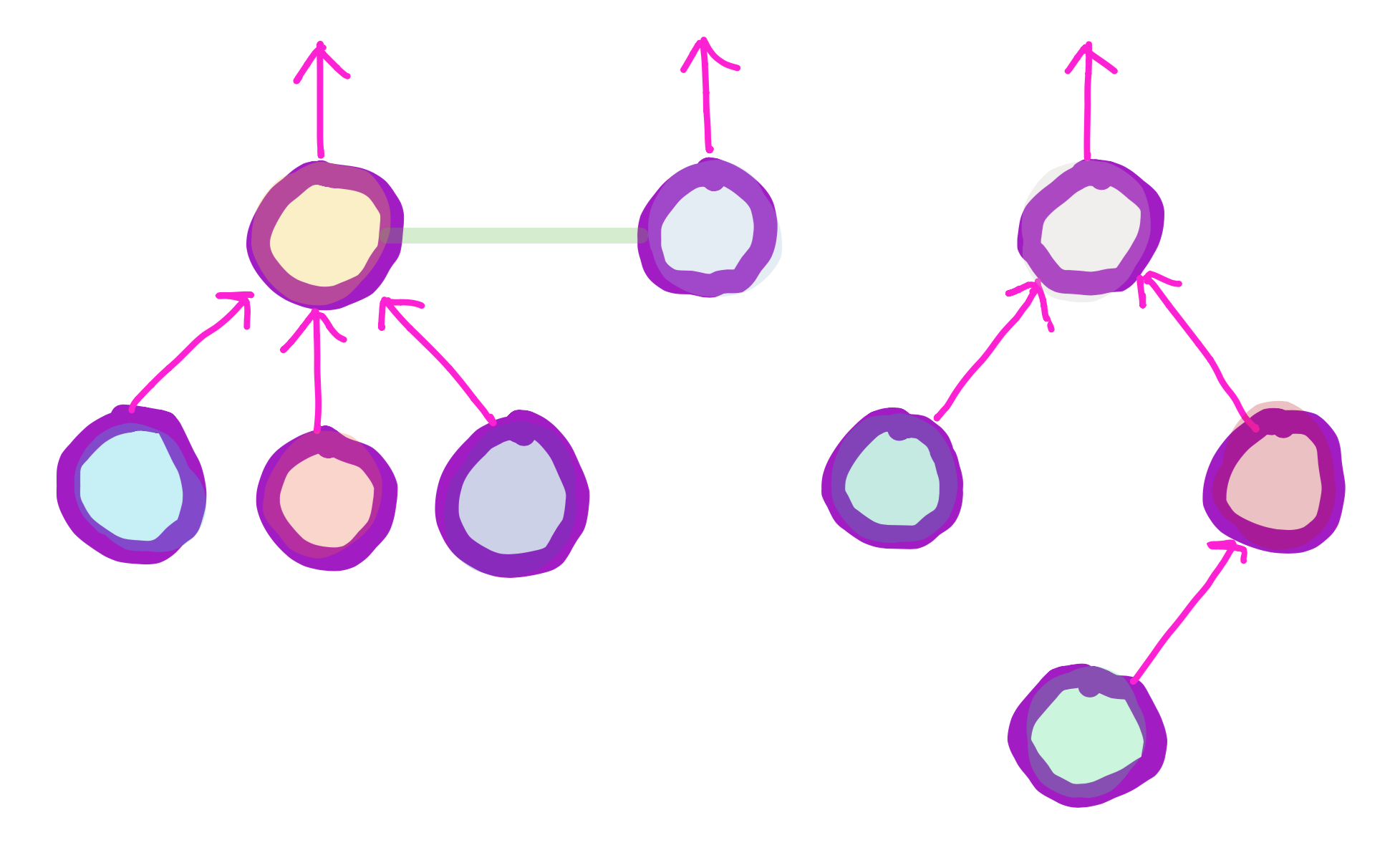
Unionize Sets
There are two types of unions
union by rank (height): minimizes the rank (height) of the disjoint sets by appending the tree of smaller rank to the root of the otherunion by size: appends the tree of smaller size to the root of the other






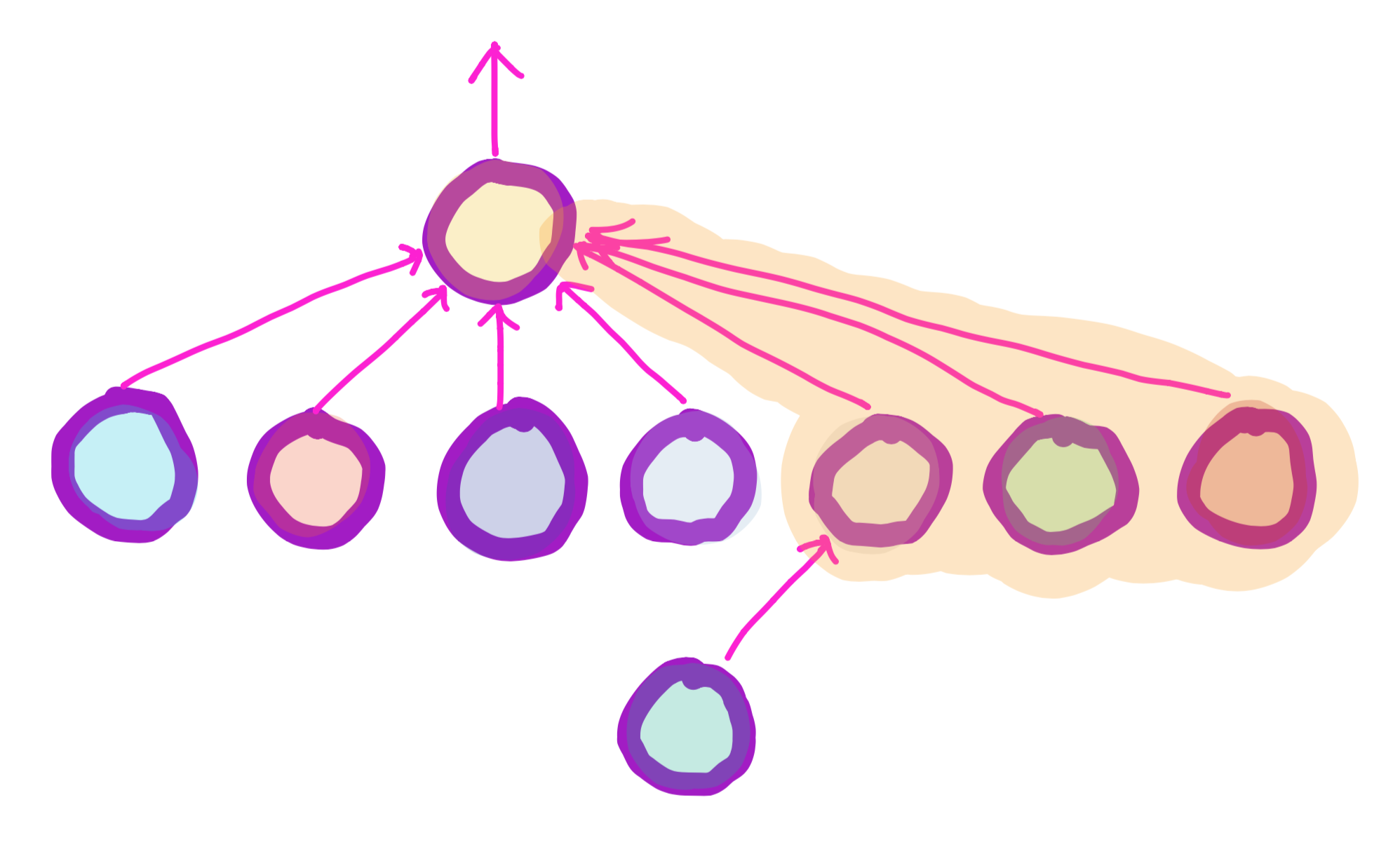
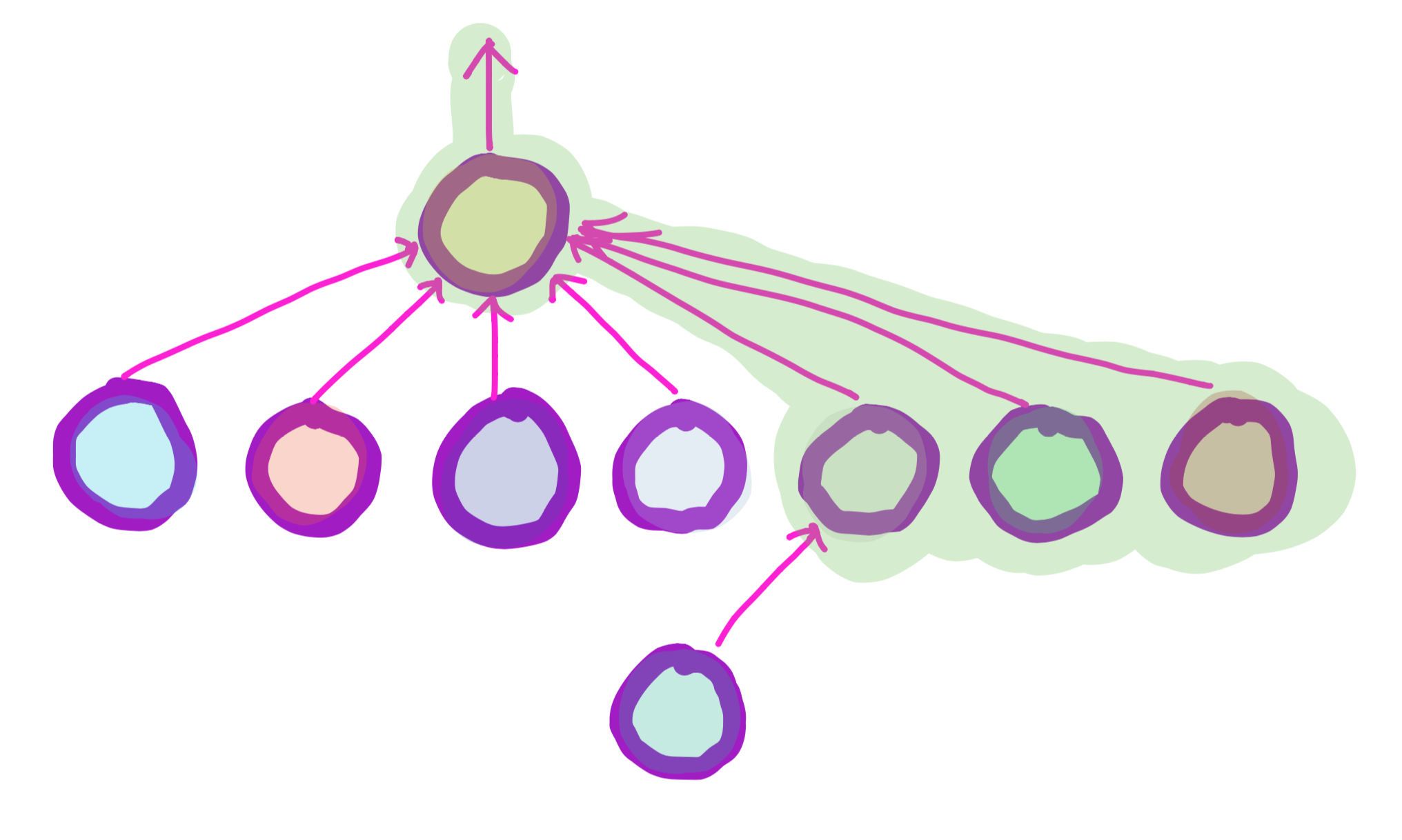
Path Compression
While finding nodes, it is efficient to move all nodes along the path of the query node to the representative node, so that the next we time we query those nodes, the runtime will be faster.


Time Complexity
With path compression and union by rank or size, the run time of the find and union operations are essentially constant time
Array Implementation
Disjoint sets can be implemented as arrays in which negative numbers indicate that they are representatives and positive numbers are pointers to their parents.
