Archived Content

This website is an archive of the Spring 2023 semester of CS 225.
→ Click here to view the current semester.
Back to Resources

Minimum Spanning Tree

by Jenny Chen

Definition

A spanning tree of a graph G is a connected acyclic subgraph of G that contains every node of G. A minimum spanning tree (MST) of a weighted graph G is a spanning tree of G which has the minimum weight sum on its edges.

Graph G
The orange highlighted subgraph is a spanning tree of G
The purple highlighted subgraph is the minimum spanning tree of weighted G

Finding the MST of a graph

There are multiple ways to find the MST of a graph. The most naive and brute force way is to try all possible subgraphs of G, find the ones that are spanning trees, then find the one with minimum weight. This would take exponential time. There are algorithms that can do this faster.

Kruskal’s Algorithm

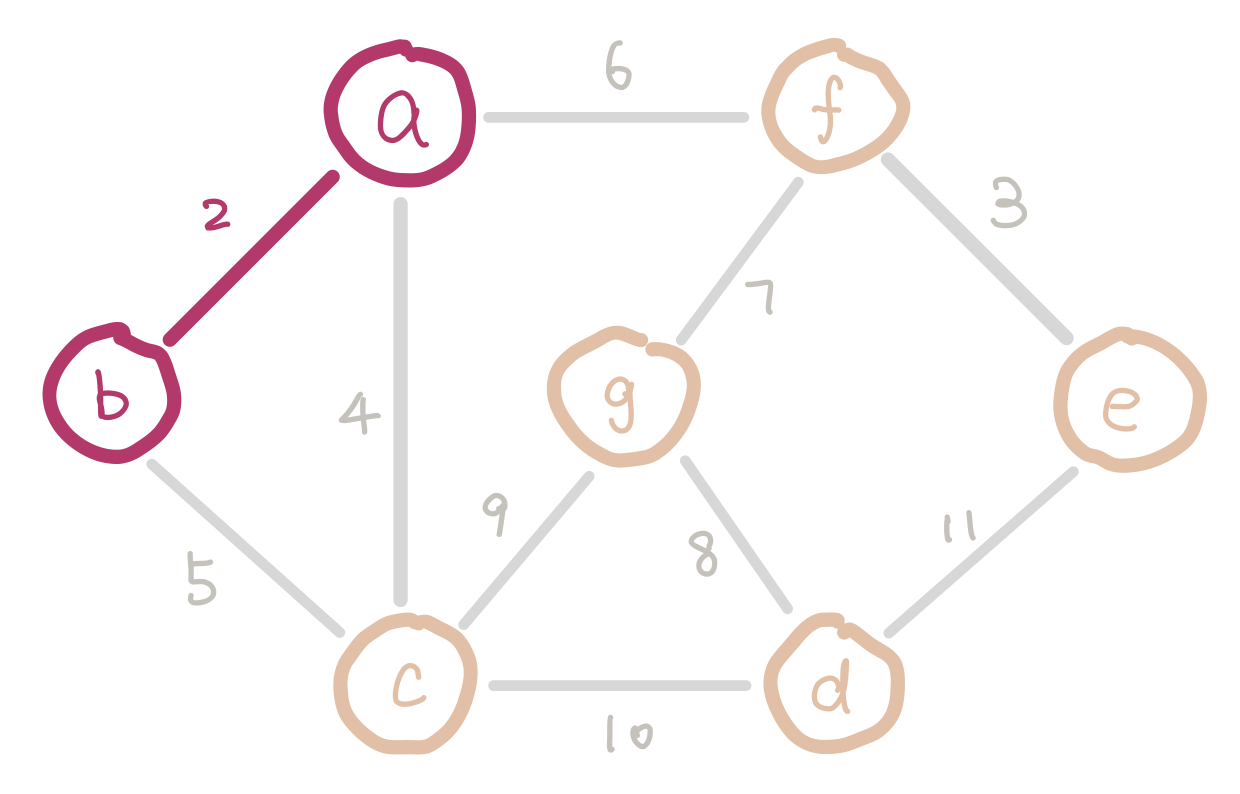
The high level idea of Kruskal’s algorithm is to build the spanning tree by inserting edges. There are two restrictions as we insert the edges:

  1. To keep the tree minimum weight, we insert the edges from low weights to high weights.
  2. To keep the tree acyclic, the edges we add must not introduce a cycle.

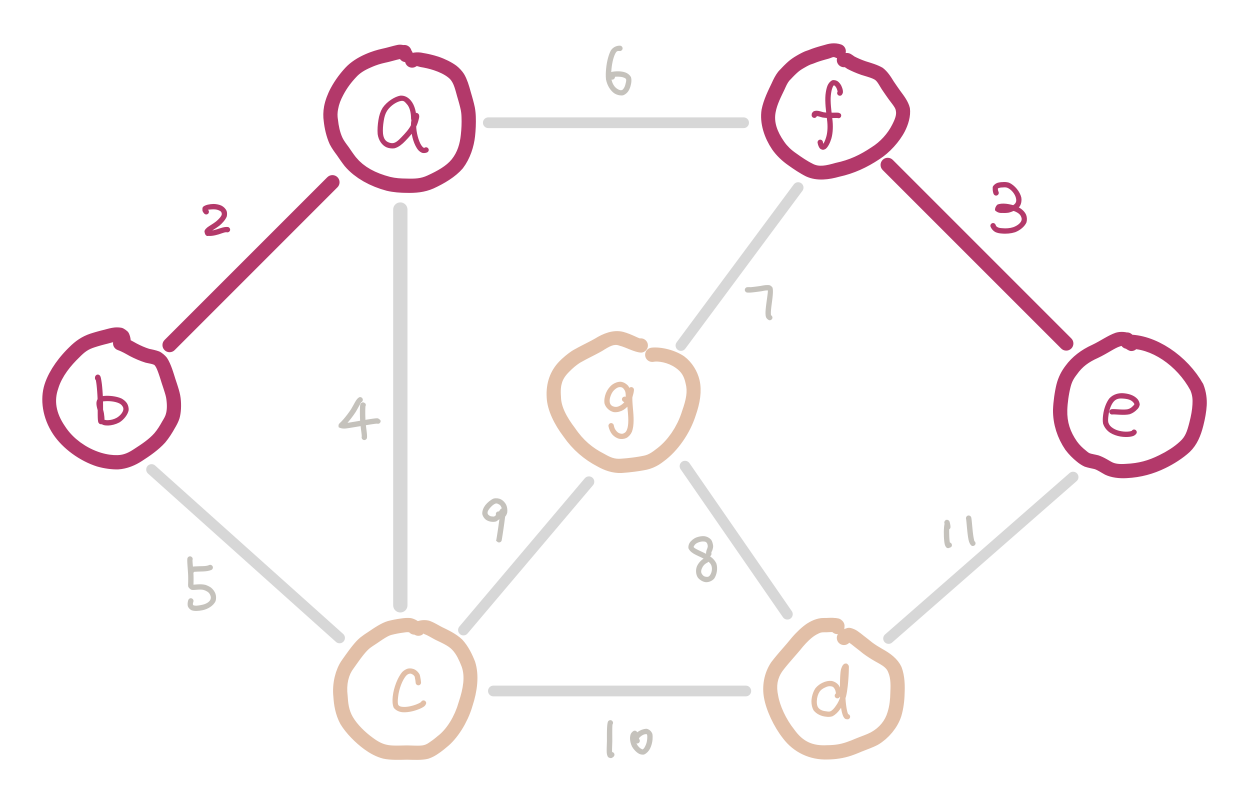
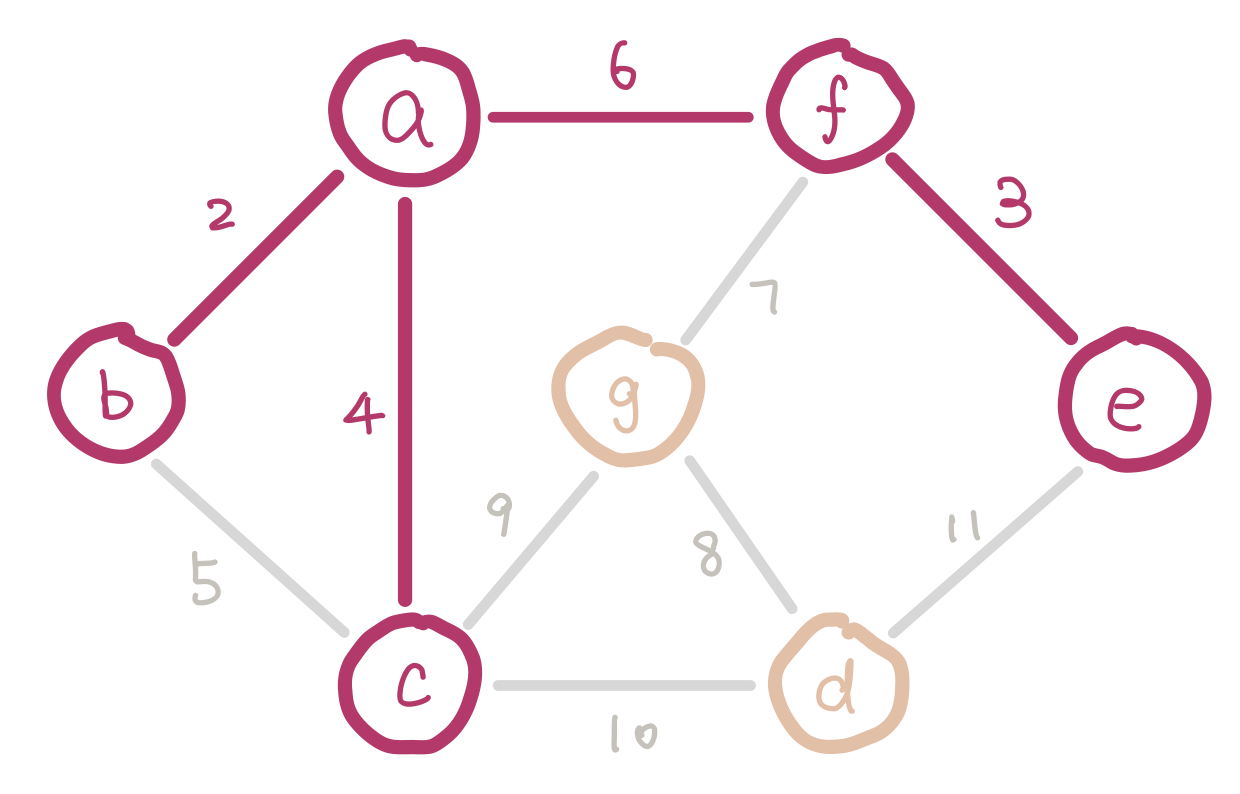
To satisfy the first condition, we sort the edges and insert them in ascending order of weight. To satisfy the second condition, we have to keep track of nodes which are already in the same connected component (smaller trees). Imagine we are half way in our algorithm. Since we are selecting edges purely by weight, there could be multiple disconnected small trees. For example our graph could look like this.

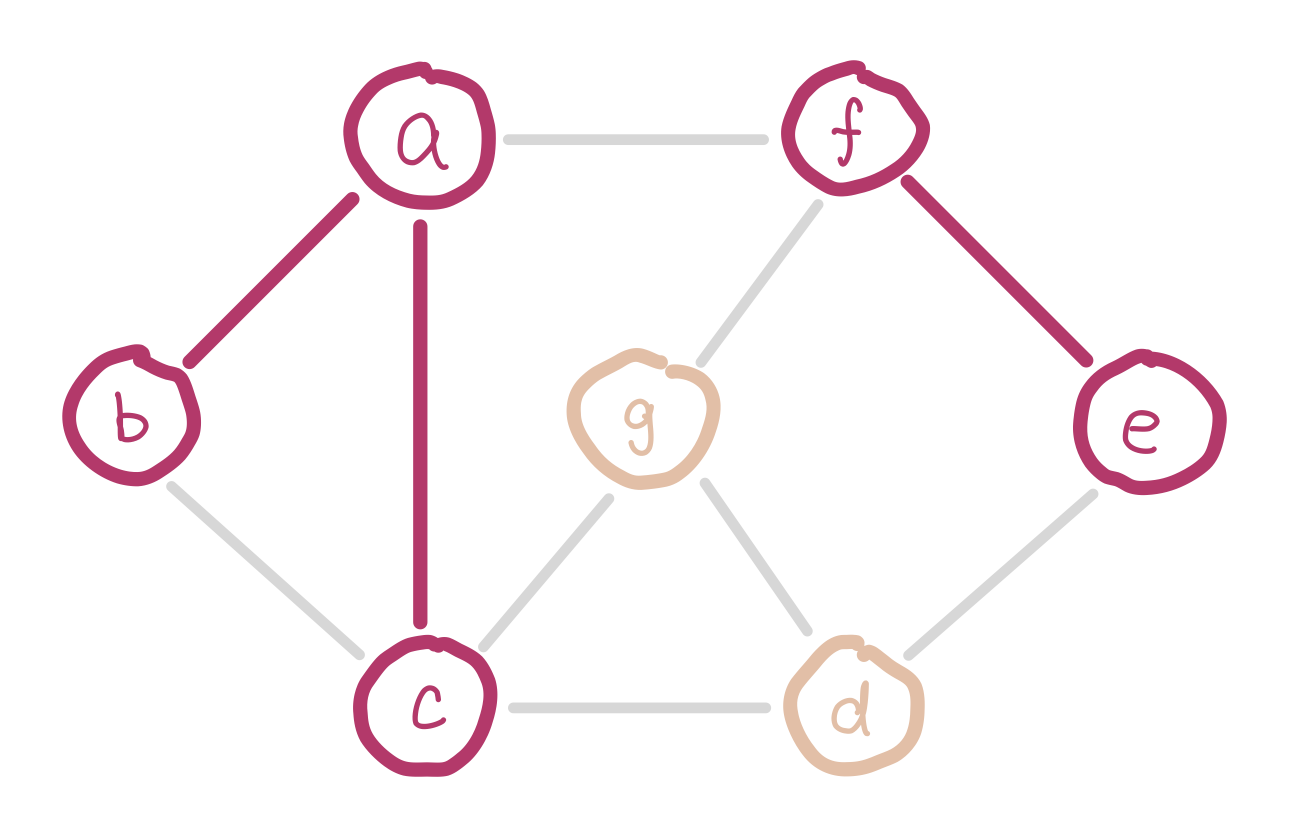
At this stage a, b, and c form a small tree, so do f and e. Inserting edge bc would introduce a cycle.

We can use disjoint sets for keeping track of which nodes are in which components. When we insert an edge, we union the two sets that the two nodes belong to. Conceptually this is adding an edge between the two small trees and merging them into a bigger tree. If the edge we are about to insert connects two nodes that are in the same set, then we cannot insert this edge because it would introduce a cycle.

A step by step example of Kruskal's Algorithm.


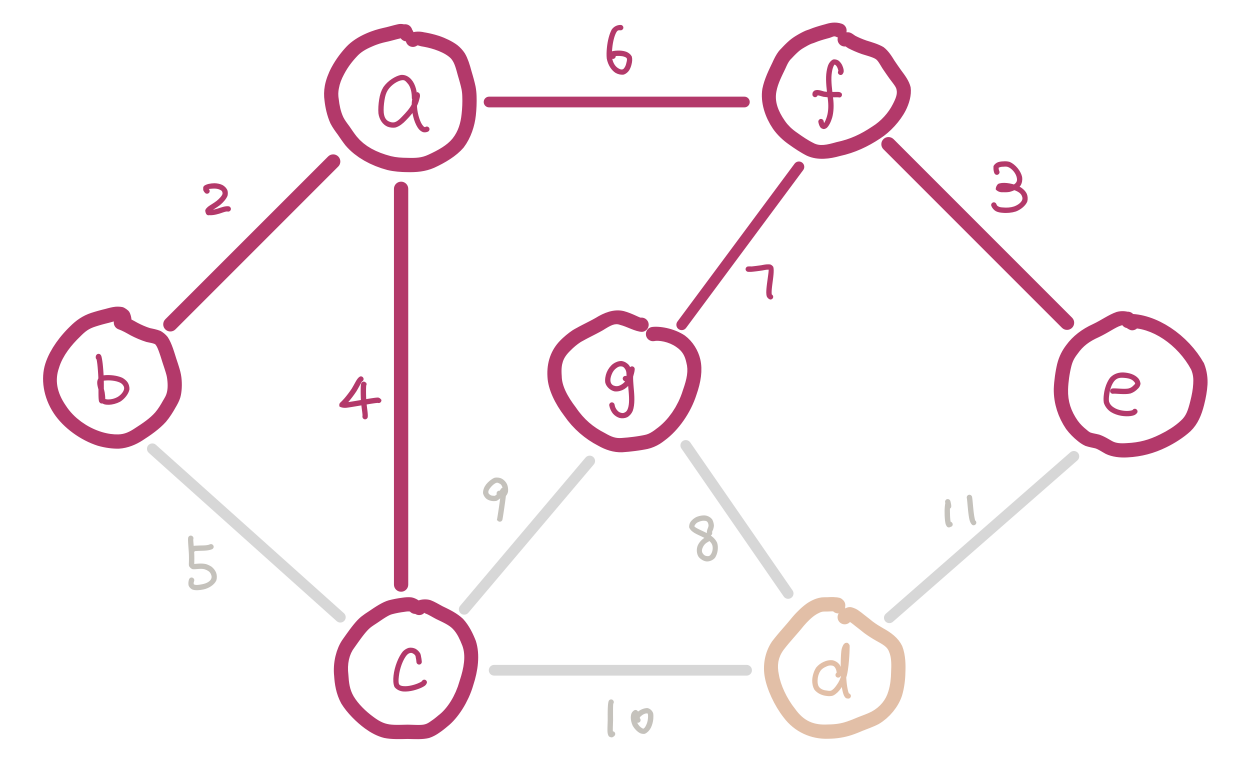
Here is the pseudocode for Kruskal’s algorithm.

1. Sort the edges in increasing order of weights
   (You can do this with a heap, or simply sort them in an array)
2. Initialize a separate disjoint set for each vertex
3. for each edge uv in sorted order:
4.   if u and v are in different sets:
5.     add uv to solution
6.     union the sets that u and v belong to

The runtime for this algorithm using either heap or sorted array are both \(O(m\cdot log(m))\), which is dominated by the sorting of edges.

Prim’s Algorithm

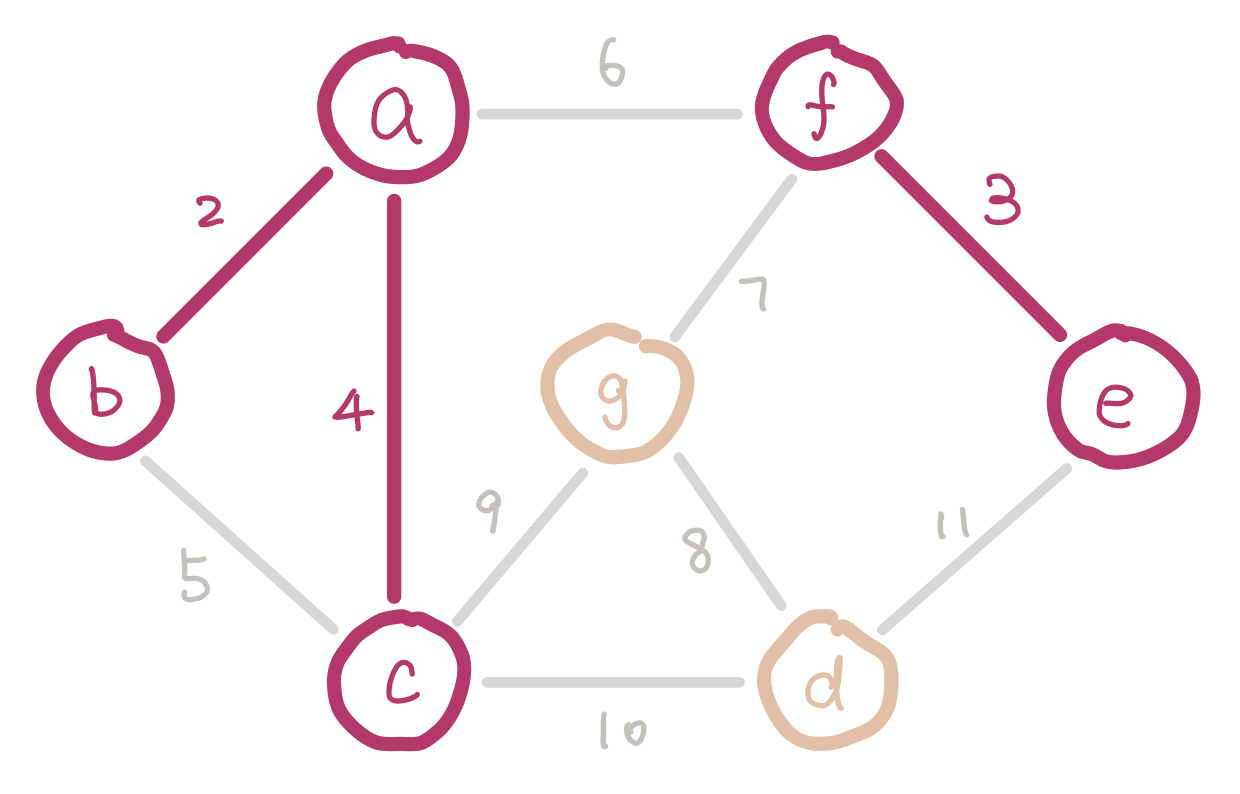
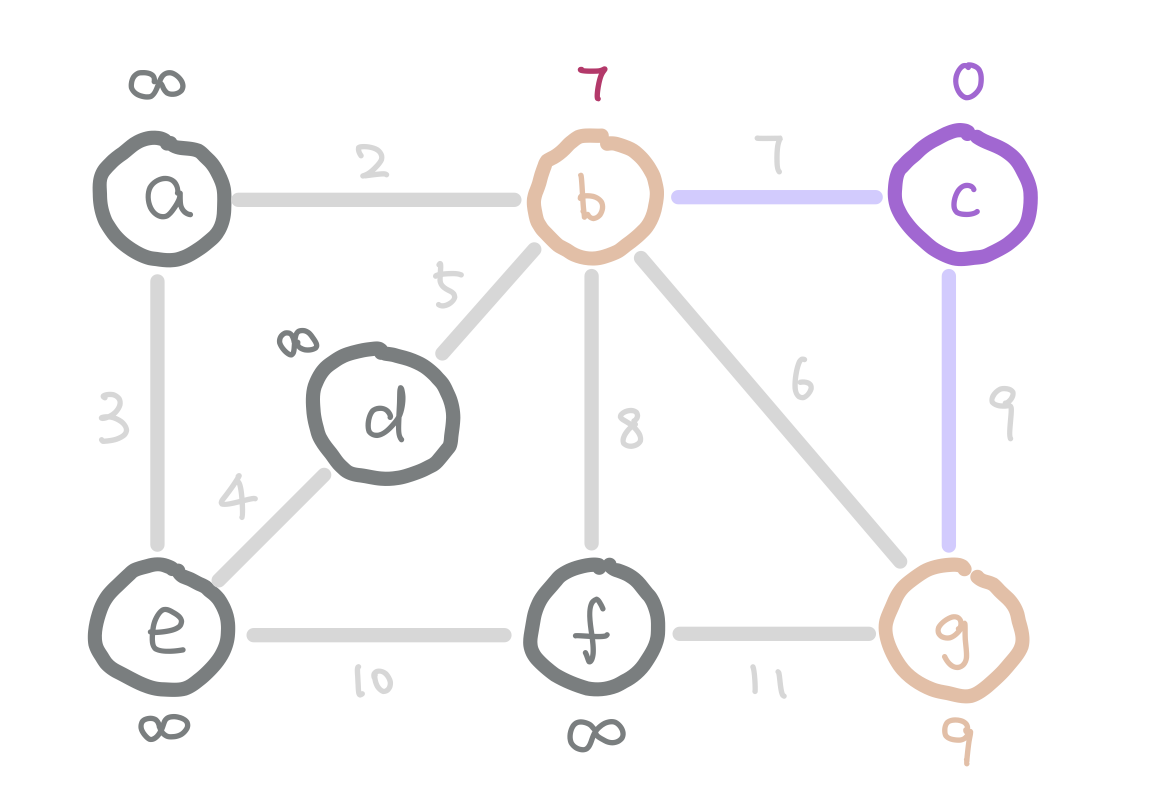
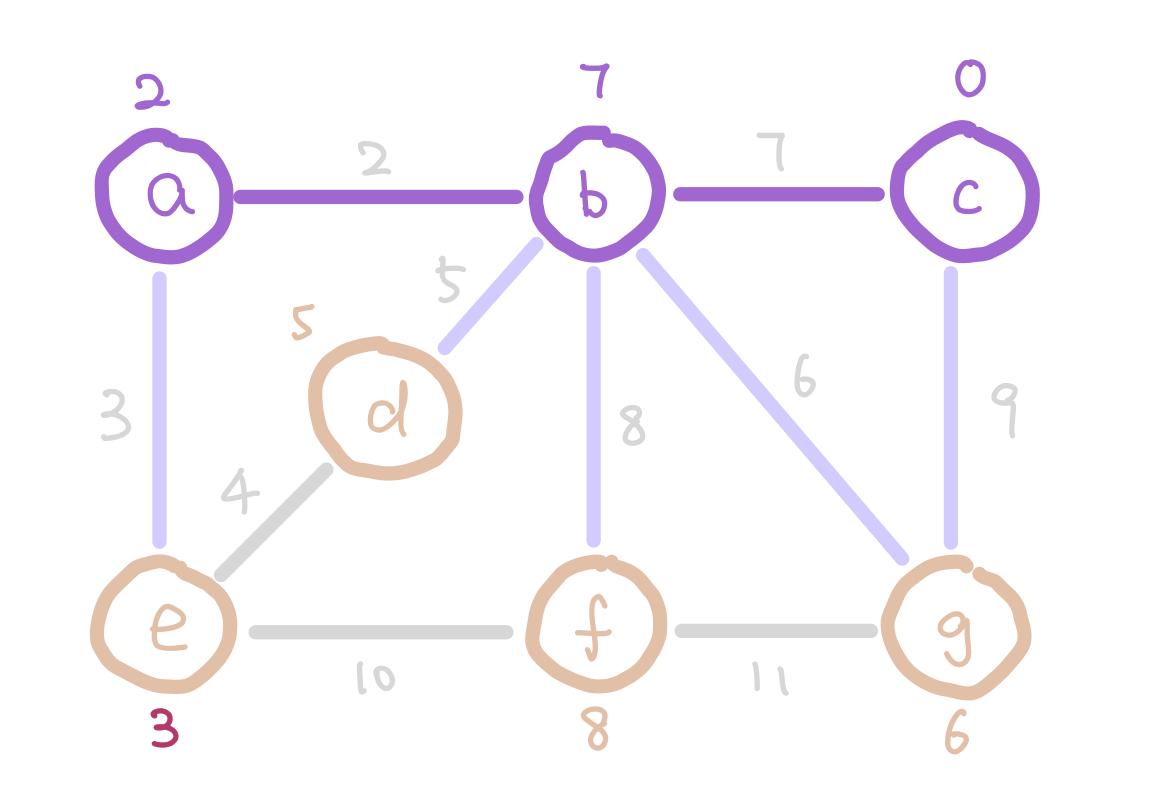
Another algorithm that finds MST efficiently is Prim’s Algorithm. The idea of Prim’s algorithm is to expand the tree by adding the smallest weight edge from “outgoing edges”. The “outgoing edges” are the edges that connect a node in our tree on one end, and a node that’s not in our tree on the other end.

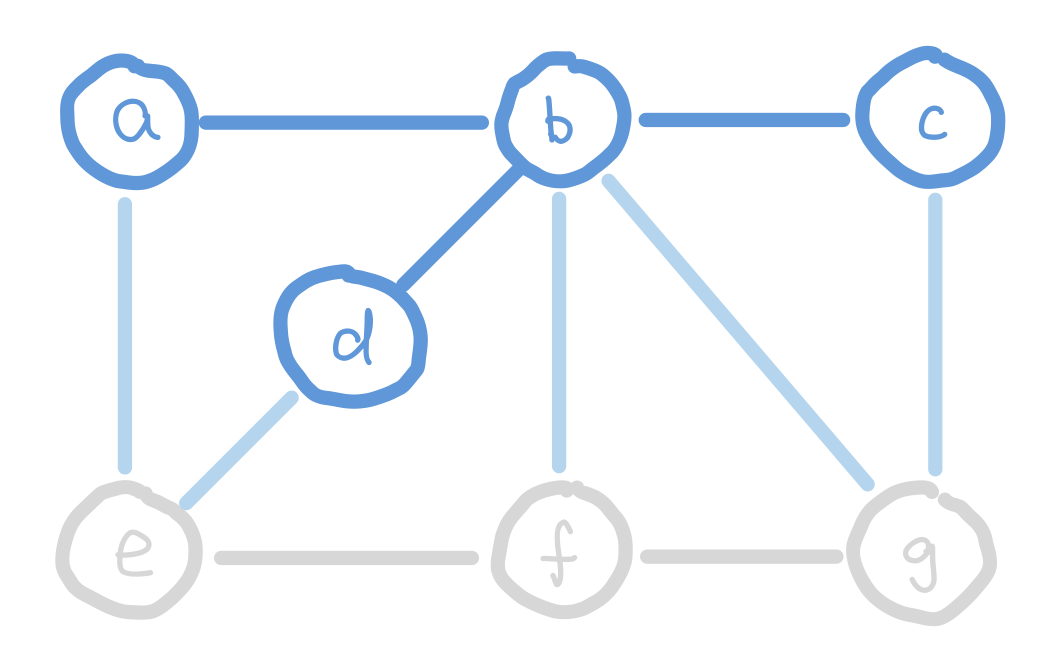
In this example, our current tree is colored with dark blue. The light blue edges are the "outgoing edges".

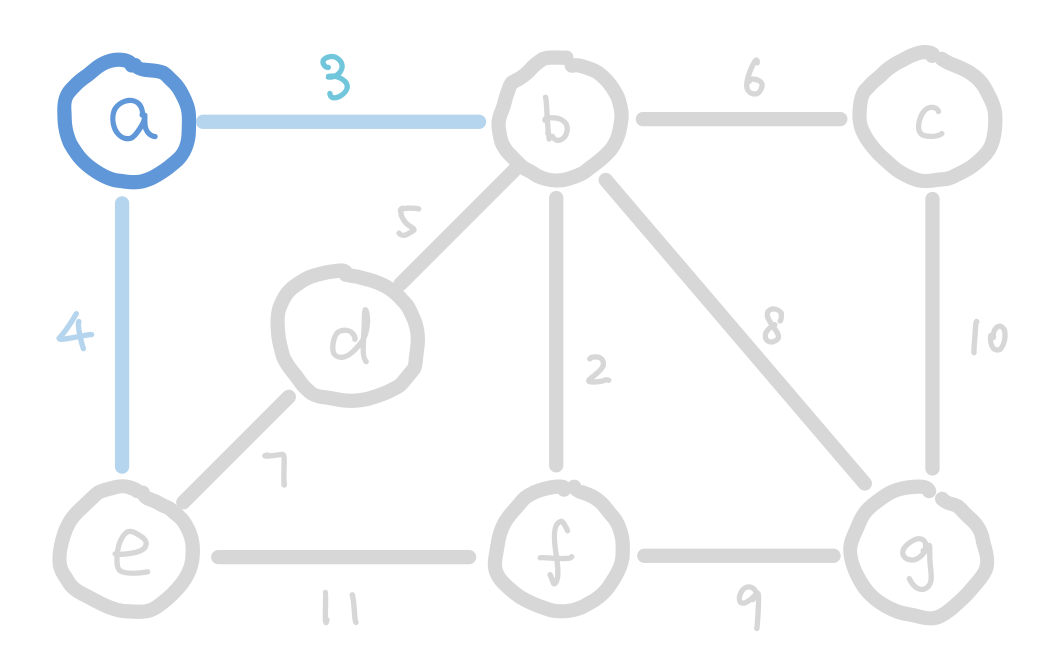
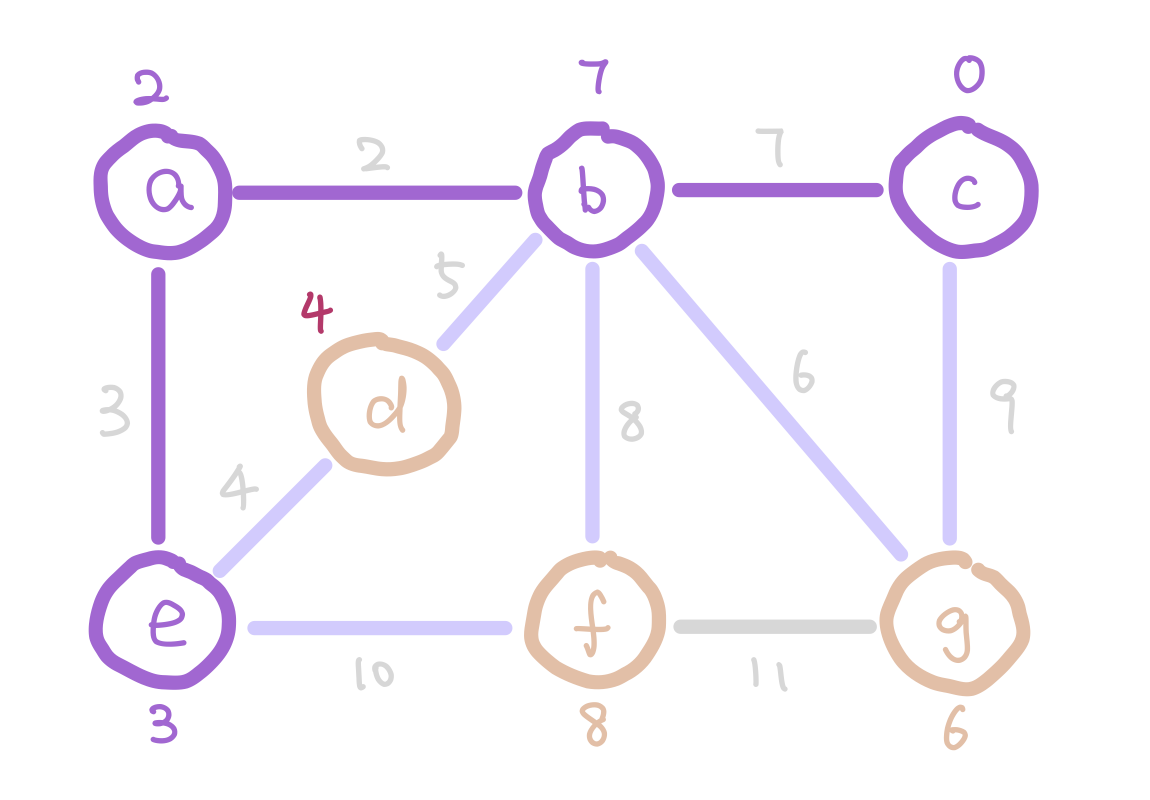
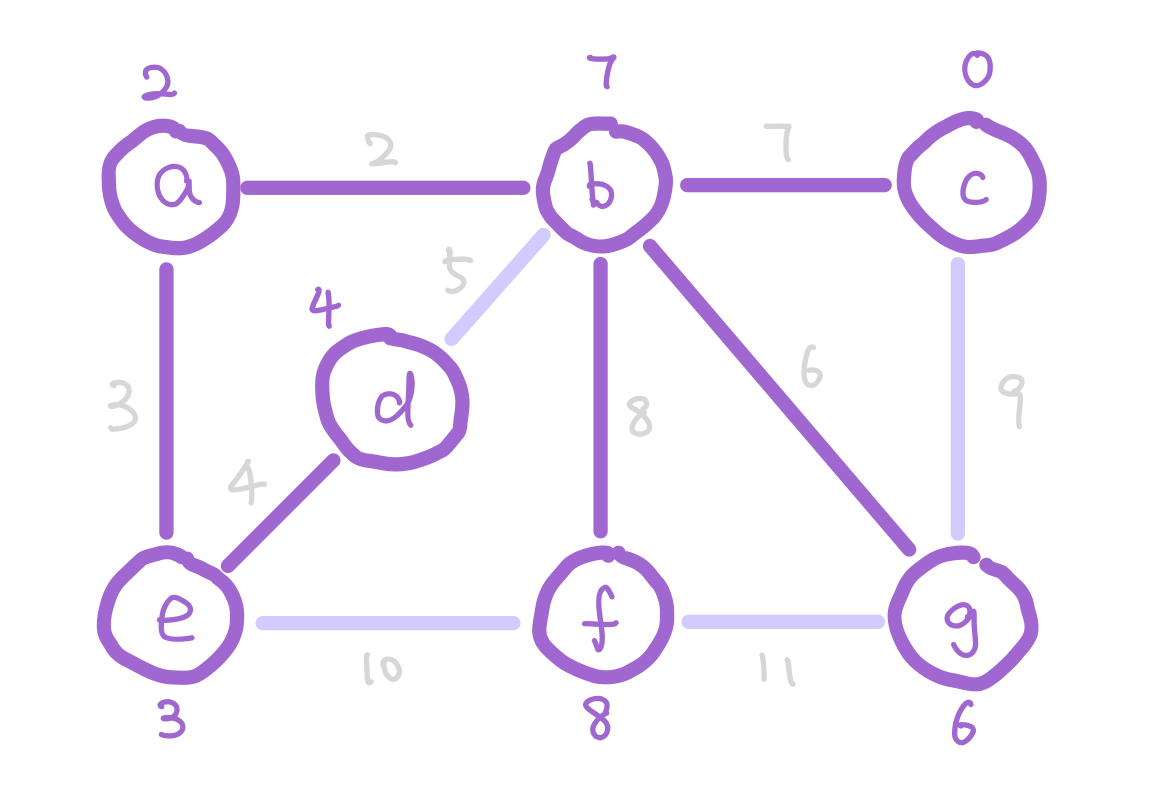
At the start of Prim’s algorithm, we choose an arbitrary node in the graph as a “starting tree”. Then for all the “outgoing edges” of our tree, we choose the one with the smallest weight and add it to our tree. This step expands our tree by one node. We keep adding edges like this until our tree contains all nodes in the graph.

One step by step example of Prim's algorithm high level idea. The dark blue edges and nodes are the current tree. The light blue edges are "outgoing edges" of our tree. The light purple edges are edges within the tree.


But how do we select the minimum “outgoing edge” in code? We can think from a different perspective. Instead of selecting from edges, we can choose from the immediate neighbor nodes of the tree. We can assign each node the minimum weight it takes to add it to our tree, and then choose the node with minimum such value. For those nodes that are not our immediate neighbors, assign them infinity so that they wouldn’t be considered. We can use the data structure heap to select the node with minimum weight efficiently.

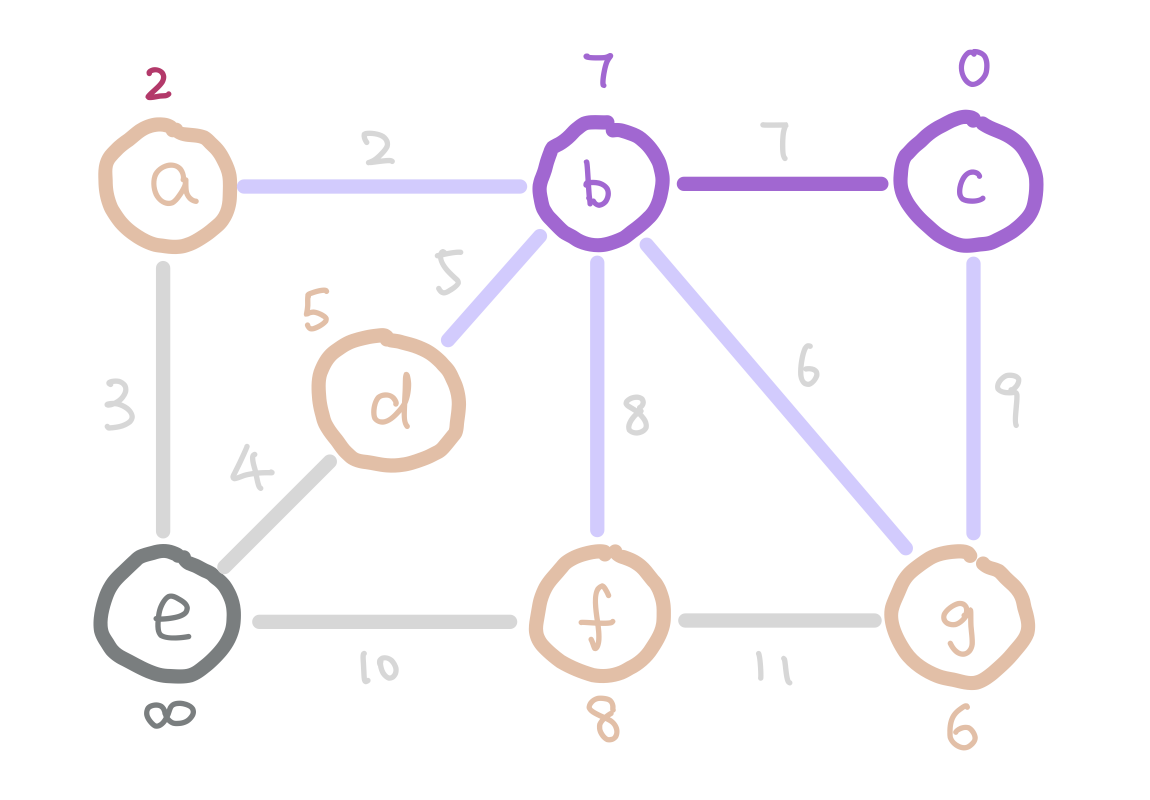
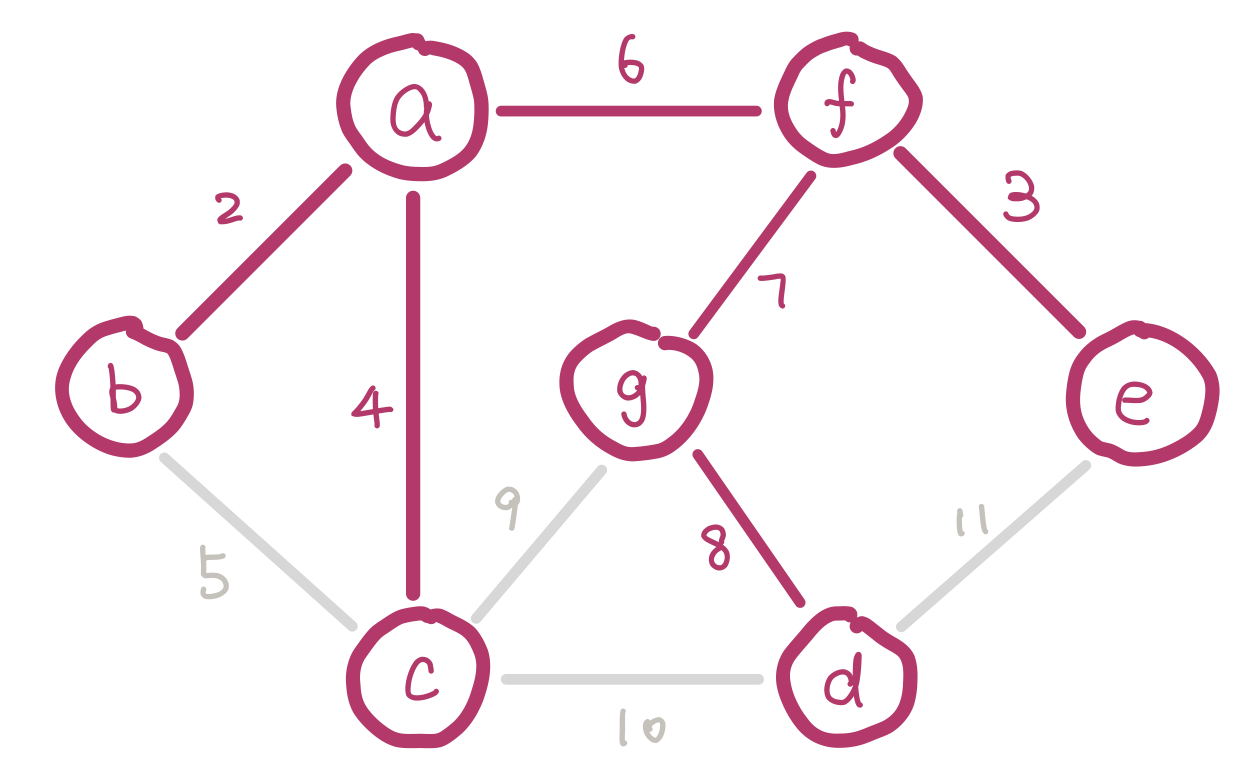
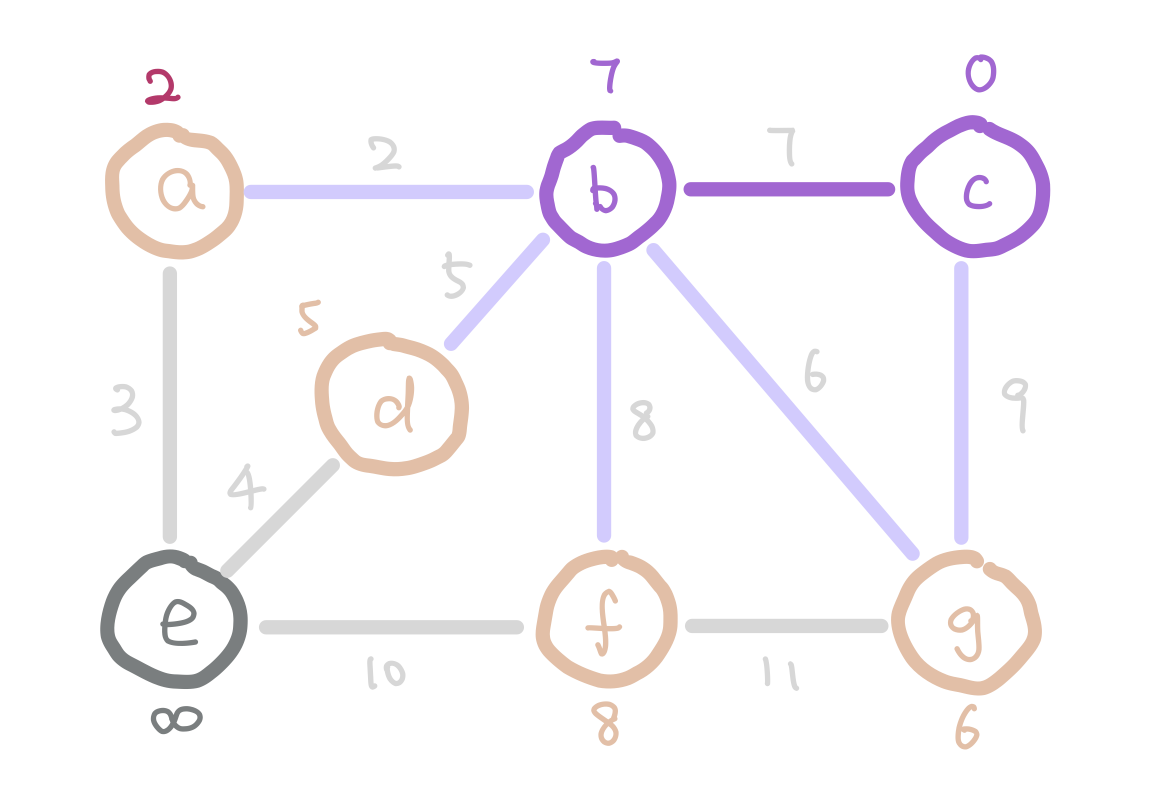
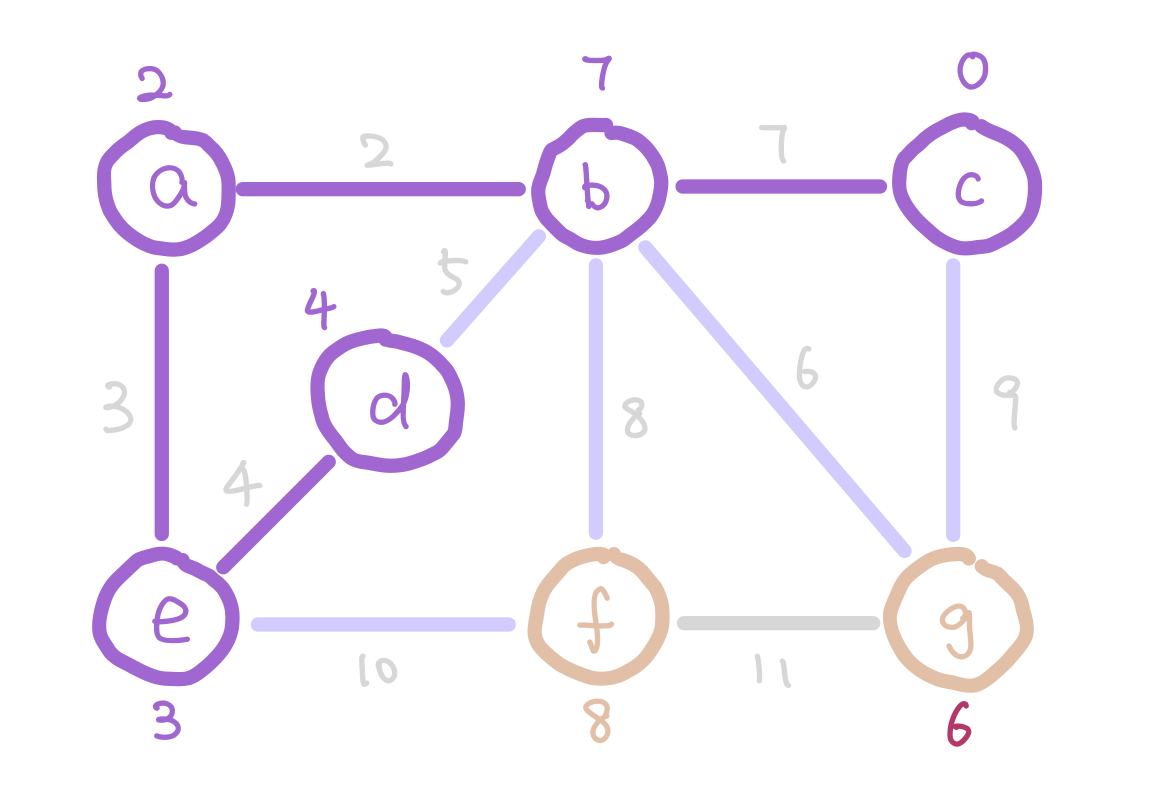
In this example, our current tree is colored with dark purple. The immediate neighbors are colored with light orange. Notice that node g has weight 6 instead of 9 because 6 is a smaller weight edge between g and our tree.

The next question is how do we update the weights on each node as the algorithm proceeds? Notice that when we add a new node into our tree, the only nodes that change weights are the neighbors of the new node we added. Therefore each time we add a node, we update the weights of the neighbors of this node.

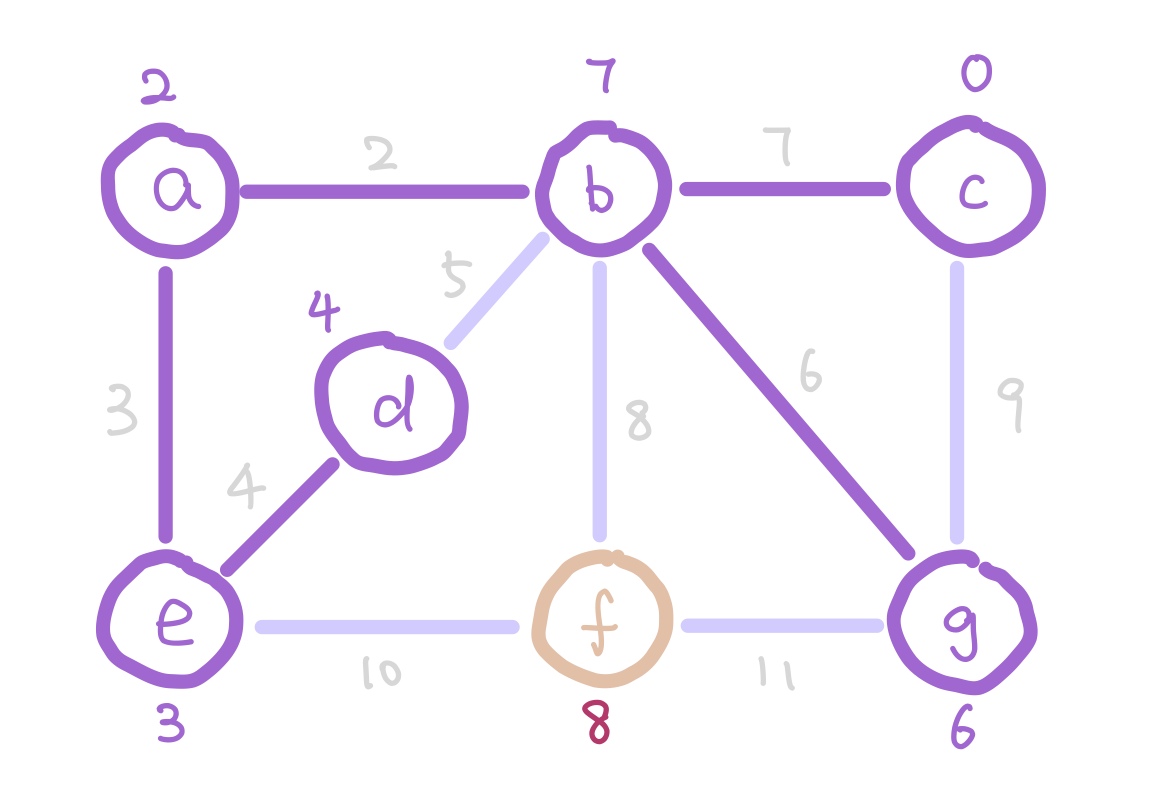
One step by step example of Prim's algorithm implementation which starts with node c.


Here is the pseudocode of Prim’s algorithm.

1. Create a heap and insert all vertices into the it with the weight infinity.
2. Choose an arbitrary node and set its weight to 0.
3. while the heap is not empty:
4.   remove the node with minimum weight from the heap, call it v
5.   add the edge that connects v and its predecessor to the solution
6.   for each neighbor u of v:
7.     if the weight of edge uv is less than the weight of u:
8.       update the weight of u to be weight of uv
9.       update u's predecessor to v

The runtime for this algorithm using a binary heap (the kind that is taught in this class) is \(O(m\cdot log(m))\). However it could be faster if we use a fibonacci heap, which can decrease its element’s priority in \(O(1)\) time. If a fibonacci heap is used, this algorithm has runtime of \(O(n\cdot log(n) + m)\).

Why do these algorithms work?

Even though both Kruskal’s and Prim’s algorithm make intuitive sense, both of them are making optimal local choices at each step. This means they are not looking at the overall graph as a whole at any time. If you are curious about “why do they work?”, take CS 374 to find out.