where F(R) = -  V(R).
V(R).
The forms of the potentials are important and discussed in Notes on Potentials.
By Molecular Dynamics, we mean the evolution of a classical equation by Newton's equation of motion. See AT pgs 1-4 for a brief history of the development of MD. In this lecture, we discuss how to solve numerically F=ma. While in nature time advances continuously, time is discrete in MD. Normally there is a fixed increment of time is denoted h throughout this lecture.
MD is the solution of md2R/dt2 = - F(R)where F(R) = -
V(R).
The forms of the potentials are important and discussed in Notes on Potentials.
Energy (E= T+V) conservation is very important. It is the basis for thermodynamics. For a numerical method to exhibit energy conservation the potential energy must be differentiable. This is often a problem at the edge of the box or when the potential is "cutoff" (a common beginner's mistake). The cuttoff must be done continuously by a procedure such as
Vc (r) = V(r) - V(rc) for r < rc, where rcis the cutoff radius.
The non-zero range of the potential should not be greater than half the dimension of simulation box, otherwise the atom would "feel" itself if periodic boundary conditions are imposed.
Please look at the code fragment to see how the simplest Lennard-Jones force calculation is programmed.
Such shifted potentials, however, do contribute to energy (with contributions changing from time-step to time-step because the number of pairs with rc varies). You must therefore account for this in the energy. Moreover, the force is discontinous at rc. (E.g. for L-J, the discontinuity is 0.039(epsilon/sigma) for rc=2.5.) This discontinuity causes numerical instabilities, which may be eliminated using a shifted-force potential, for example.
Vsf(r)=V(r) - V(rc) -Gradient term now makes force continuous and zero beyong cut-off. Note that this really is a different potential now and you must recover original thermodynamics, or be statisified with current model. (Recover of thermodynamics can be done in some cases by perturbation theory.)V(rc)(r-rc) for r .le. rc and 0 for r .gt. rc.
A & T pgs. 71-84
Criteria for selecting an integrator:
Some additional questions:
Characteristics of simulations which affect choice of estimator.
The nearly universal choice for an integrator is the Verlet algorithm (L. Verlet, Phys. Rev. 159, 98 (1967)).
Let us make a Taylor solution of trajectory about the current position:
r(t+h) = r(t) + v(t) h + 1/2 a(t) h2 + b(t) h3 + O(h4)
Substitute in for -t:
r(t-h) = r(t) - v(t) h + 1/2 a(t) h2 - b(t) h3 + O(h4)
Add the two expansions:
r(t+h) = 2 r(t) - r(t-h) + a(t) h2 + O(h4)
Velocities are eliminated. One can estimate them as:
v(t) = (r(t+h) - r(t-h))/(2h) + O(h2)
Time reversal invariance and momentum conservation are built in. This implies that the energy has no drift. Probably the dynamics generated by the Verlet algorithm has a constant of motion which is nearly but not exactly equal to the total energy.
Homework a. Prove that the Verlet algorithm is time-reversal invariant. That is, show that if we use r(t+h) and r(t) as inputs we get r(t-h) (up to round-off errors). Why does this form have a possible problem with round-off errors?
Velocity Verlet is algebraically equivalent but avoids taking differences between large numbers.
r(t+h) = r(t) + v(t) h + 1/2 a(t) h2 v(t+h) = v(t) + 1/2 (a(t) + a(t+h))h
Homework b. Prove that this is equivalent.
Higher order algorithms are available (Gear etc.) These are useful only when high accuracy is needed and the potential and several derivatives are smooth.
The graph below from Berendsen and van Gunsteren (in MD simulation of Statistical-Mechanical Systems , 1986) shows a study of energy conservation versus time step for the Verlet algorithm and higher order Gear algorithms on a protein. If is seen that for large time steps the Verlet algorithm is considerably more stable. Higher order algorithms have only a the marginal increase in efficiency and actually get worse beyond 7th order.
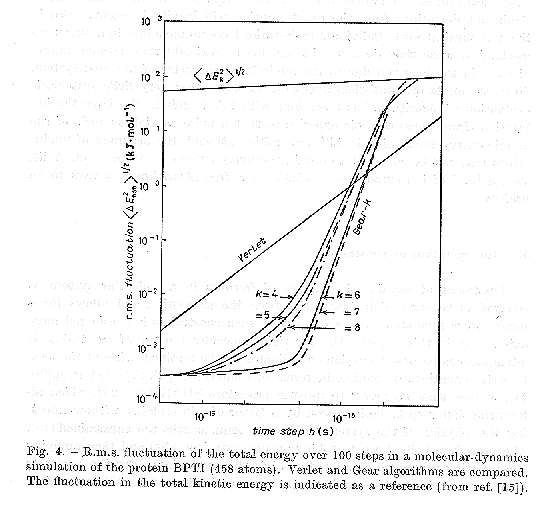
The following quote is from their article:
How accurate a simulation has to be in order to provide reliable statistical results is still a matter of debate. The purpose is never to produce reliable trajectories. Whatever accuracy the forces and the algorithms have, significant deviations from the exact solution will inevitably occur. Also in the real physical world individual trajectories have no meaning: in a quantum mechanical sense they do not exist and even classically they become unpredictable in the long run due to the nonisolated character of any real system. So what counts are statistical averages. It seems that very little systematic evaluation of algorithms has been done with this in mind. We have the impression that a noise as high as 10% of the kinetic energy fluctuation is still acceptable, although the accuracy of fluctuations may not be sufficient to obtain thermodynamic date from them. With such a level of inaccuracy the Verlet of leap frog algorithm is always to be preferred.