Physics 150
Basic Math
Algebra
The primary skill of algebra you will need for this course is to be able
to solve for a desired variable in an equation or formula involving numbers
and/or variables.
Notation
You will need to be familiar with the following notation:
-
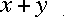 means
"x plus y"
means
"x plus y"
-
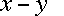 means
"x minus y"
means
"x minus y"
-
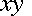 or
or  means "x times y"
means "x times y"
-
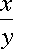 means "x
divided by y"
means "x
divided by y"
-
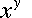 means "x to the y power,"
or "x times itself y times." So,
means "x to the y power,"
or "x times itself y times." So, 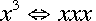 ,
where
,
where  means "is the
same as"
means "is the
same as"
-
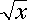 means "the square root
of x." Note that
means "the square root
of x." Note that  .
.
-
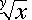 means "the yth root
of x." Note that
means "the yth root
of x." Note that  .
.
Basic Manipulation
There are a few rules that you use in algebra to manipulate equations.
We use these rules to go from one equation, which has a form we don't like,
to another equation which has a form we want. When we use these rules to
isolate a particular variable on one side of the equation, we call that
"solving for" that variable. The rules of manipulation are:
-
You can add or subtract zero from anything. So,
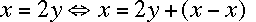 because
because  .
.
-
You can multiply or divide anything by 1. So,
 because
because 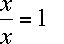 .
.
-
You can perform any operation on an equation as long as you apply it to
both sides of the equation. So,
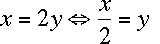 ,
because we divided both sides of the equation by the same number (2), and
,
because we divided both sides of the equation by the same number (2), and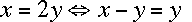 because we subtracted the same variable from both sides of the equation.
because we subtracted the same variable from both sides of the equation.
-
When multiplying powers of a number, add the exponents, and when
dividing powers subtract the exponents. Thus,
 ,
and
,
and 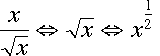 .
.
Some Examples
-
Solve for
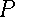 in the equation
in the equation 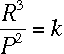 :
:
-
First, multiply both sides by
 .
So,
.
So, 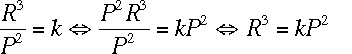 .
.
-
Next, divide both sides by
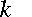 .
So,
.
So, 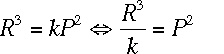 .
.
-
Finally, take the square root of both sides, which leaves you with just
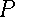 :
: 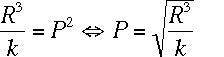 .
.
-
Now, if you want to know a numerical value for
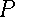 ,
you have to know numerical values for
,
you have to know numerical values for 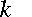 and
and 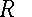 . Let's suppose
that
. Let's suppose
that 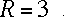 and
and 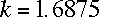 .
Just plug those numbers into a scientific calculator, and you get
.
Just plug those numbers into a scientific calculator, and you get  .
.
-
Solve for
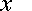 in the equation
in the equation 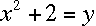 :
:
-
Subtract 2 from both sides, so

-
Take the square root of both sides, so
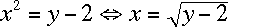 .
That's it!
.
That's it!
-
If you want a numerical value for
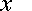 ,
you need to know
,
you need to know  .
Note that not every value of
.
Note that not every value of  will work....if
will work....if 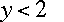 ,
then you'll be taking the square root of a negative number....something
we don't know how to do in this class....
,
then you'll be taking the square root of a negative number....something
we don't know how to do in this class....
Scientific Notation
When dealing with very large or very small numbers, it is much more convenient
(and takes a lot less typing) to use Scientific Notation. Scientific notation
takes the form 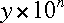 ,
and the rule is quite simple. If
,
and the rule is quite simple. If 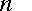 is positive, move the decimal point
is positive, move the decimal point 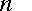 places to the right. If
places to the right. If 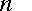 is negative, move the decimal point
is negative, move the decimal point 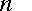 places to the left. When typing, we often abbreviate scientific notation
with an "e" instead of the
places to the left. When typing, we often abbreviate scientific notation
with an "e" instead of the 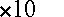 .
Some examples:
.
Some examples:
-
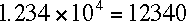 = 1.234e+4
= 1.234e+4
-
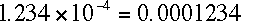 = 1.234e-4
= 1.234e-4
-
 = 1.234e+0
= 1.234e+0
-
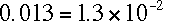 = 1.3e-2
= 1.3e-2
-
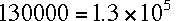 = 1.3e+5
= 1.3e+5
Geometry
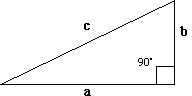 The
main fact that we will use in geometry is the Pythagorean Theorem. The
Pythagorean Theorem is quite simple. Suppose you have a triangle like the
one at the left. The Pythagorean Theorem says that the square of the length
of the hypotenuse (the side opposite the right angle) is equal to the sum
of the squares of the other two sides. So,
The
main fact that we will use in geometry is the Pythagorean Theorem. The
Pythagorean Theorem is quite simple. Suppose you have a triangle like the
one at the left. The Pythagorean Theorem says that the square of the length
of the hypotenuse (the side opposite the right angle) is equal to the sum
of the squares of the other two sides. So,  .
Some examples:
.
Some examples:
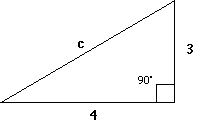
-
Find the length of the unknown side of the triangle to the right. Since
this is the hypotenuse, we just use a little algebra, and find that
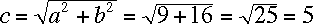 .
.
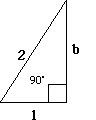
-
Find the length of the unknown side of the triangle to the right. This
time, it isn't the hypotenuse, but the algebra isn't much more difficult.
With not much work, we find that
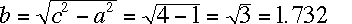 .
.
-
Note that if the triangle isn't a right triangle (a right triangle has
one angle exactly ninety degrees), we can still solve for the length of
any side, given the lengths of the other two sides and the angles of the
triangle. But, it is a lot more difficult, and we won't do that in this
class....
Back to the Physics 150 Home Page
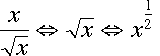 .
.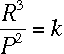 :
: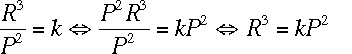 .
.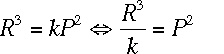 .
.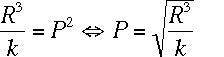 .
. .
. The
main fact that we will use in geometry is the Pythagorean Theorem. The
Pythagorean Theorem is quite simple. Suppose you have a triangle like the
one at the left. The Pythagorean Theorem says that the square of the length
of the hypotenuse (the side opposite the right angle) is equal to the sum
of the squares of the other two sides. So,
The
main fact that we will use in geometry is the Pythagorean Theorem. The
Pythagorean Theorem is quite simple. Suppose you have a triangle like the
one at the left. The Pythagorean Theorem says that the square of the length
of the hypotenuse (the side opposite the right angle) is equal to the sum
of the squares of the other two sides. So, 
