 Energetics of
a Cart Rolling Down an Incline, Stretching a Spring
Energetics of
a Cart Rolling Down an Incline, Stretching a Spring
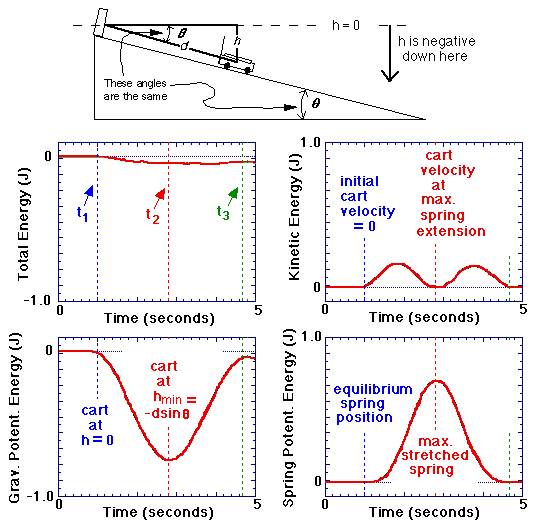 At t = t1: the cart is at the origin, h=0, so the cart's
gravitational potential energy, mgh is zero; the spring is at its
equilibrium length, so the spring potential energy,
1/2k x2 is zero; the cart's initial
velocity is zero, so the cart's kinetic energy is zero.
For t1 < t < t2: the cart starts rolling down
the incline, so the cart's kinetic energy first increases, then attains
its maximum value before decreasing towards zero; the spring's potential
energy increases as the spring stretches beyond its equilibrium value;
and the cart's potential energy, mgh, decreases as the cart's height
decreases according to, h = -dsinØ. At t = t2: the
spring attains its maximum extension, so the spring's potential energy,
1/2k x2, is a maximum; the cart stops
momentarily before returning up the incline for t > t2; th
cart attains its largest distance below the origin, hmin =
-dmaxsinØ, and thus the cart's gravitational potential
energy attains it's maximum negative value. The cycle repeats for
t > t3 (Lecture 10).
At t = t1: the cart is at the origin, h=0, so the cart's
gravitational potential energy, mgh is zero; the spring is at its
equilibrium length, so the spring potential energy,
1/2k x2 is zero; the cart's initial
velocity is zero, so the cart's kinetic energy is zero.
For t1 < t < t2: the cart starts rolling down
the incline, so the cart's kinetic energy first increases, then attains
its maximum value before decreasing towards zero; the spring's potential
energy increases as the spring stretches beyond its equilibrium value;
and the cart's potential energy, mgh, decreases as the cart's height
decreases according to, h = -dsinØ. At t = t2: the
spring attains its maximum extension, so the spring's potential energy,
1/2k x2, is a maximum; the cart stops
momentarily before returning up the incline for t > t2; th
cart attains its largest distance below the origin, hmin =
-dmaxsinØ, and thus the cart's gravitational potential
energy attains it's maximum negative value. The cycle repeats for
t > t3 (Lecture 10).
 At t = t1: the cart is at the origin, h=0, so the cart's
gravitational potential energy, mgh is zero; the spring is at its
equilibrium length, so the spring potential energy,
1/2k x2 is zero; the cart's initial
velocity is zero, so the cart's kinetic energy is zero.
For t1 < t < t2: the cart starts rolling down
the incline, so the cart's kinetic energy first increases, then attains
its maximum value before decreasing towards zero; the spring's potential
energy increases as the spring stretches beyond its equilibrium value;
and the cart's potential energy, mgh, decreases as the cart's height
decreases according to, h = -dsinØ. At t = t2: the
spring attains its maximum extension, so the spring's potential energy,
1/2k x2, is a maximum; the cart stops
momentarily before returning up the incline for t > t2; th
cart attains its largest distance below the origin, hmin =
-dmaxsinØ, and thus the cart's gravitational potential
energy attains it's maximum negative value. The cycle repeats for
t > t3 (Lecture 10).
At t = t1: the cart is at the origin, h=0, so the cart's
gravitational potential energy, mgh is zero; the spring is at its
equilibrium length, so the spring potential energy,
1/2k x2 is zero; the cart's initial
velocity is zero, so the cart's kinetic energy is zero.
For t1 < t < t2: the cart starts rolling down
the incline, so the cart's kinetic energy first increases, then attains
its maximum value before decreasing towards zero; the spring's potential
energy increases as the spring stretches beyond its equilibrium value;
and the cart's potential energy, mgh, decreases as the cart's height
decreases according to, h = -dsinØ. At t = t2: the
spring attains its maximum extension, so the spring's potential energy,
1/2k x2, is a maximum; the cart stops
momentarily before returning up the incline for t > t2; th
cart attains its largest distance below the origin, hmin =
-dmaxsinØ, and thus the cart's gravitational potential
energy attains it's maximum negative value. The cycle repeats for
t > t3 (Lecture 10).