Last (Lab #4) Next (Lab #6) Lab Page

Physics 111 Lab #5:

Collisions

Key Activities:

Nearly Elastic Collisions

The first activity will involve studying nearly elastic collisions (Lectures 15, 16) including a "no-contact" collision (via magnetic repulsion) between a cart and a barrier (Collision A).

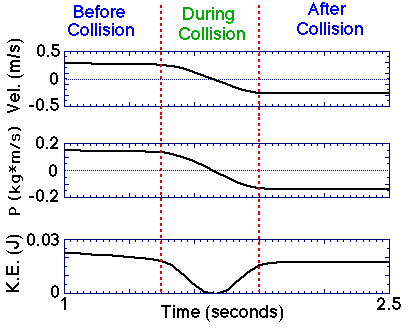
Using a motion detector, the velocity (top), momentum (middle), and kinetic energy (bottom) of the cart is studied before, during, and after the collision (in this case, Collision A). An analysis of this data shows that this collision exhibits a roughly 10% loss of kinetic energy due to the collision. This energy is primarily lost to the barrier due to the "recoil" motion of the barrier during the collision.

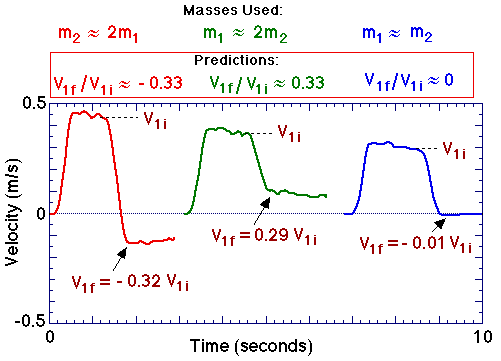
An elastic collision between a moving "incident" cart and a stationary "target" cart will also be studied. The ratio between the "incident" cart's final and initial velocities, v_1f/v_1i, will be studied as a function of the "incident" and "target" cart's masses. In an ideal elastic collision, in which momentum is conserved and the relative velocity between the two carts is unchanged by the collision, one expects v_1f/v_1i = (m₁ - m₂)/(m₁ + m₂).

Impulsive Collisions

In this activity, different impulsive forces and their relationship to momentum change will be investigated (Lecture 16).

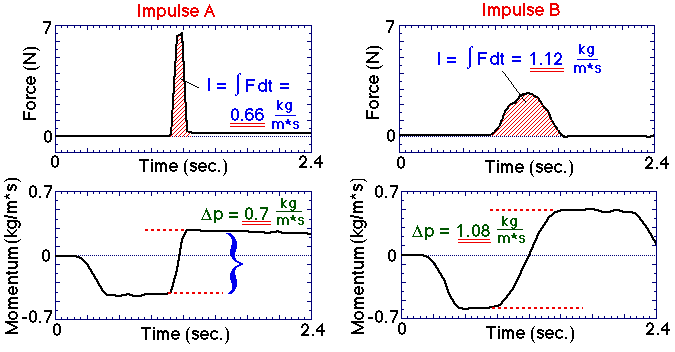Using a motion detector and a force probe, the force vs. time profile of different impulsive forces will be measured, integrated, then compared to the observed change in the cart's momentum. The left pair of force and momentum plots correspond to the impulse generated with the string alone (Impulse A), while the right pair correspond to the impulse generated when a spring is added (Impulse B). Both impulse experiments demonstrate (a) the equivalence between the change in momentum, p_f - p_i, and the impulse, I (= area under the F(t) curve), and (b) the insensitivity of this equivalence to the shape of the F(t) curve.

Inelastic Collisions

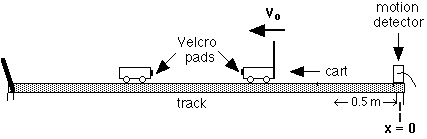
The change in cart momentum and kinetic energy through a completely inelastic collision with another cart will also be investigated (Lecture 14).

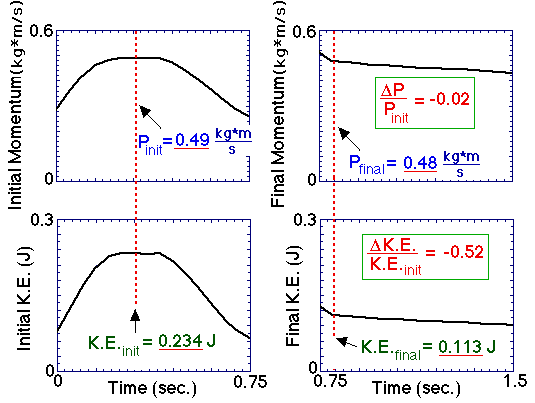
The data shown illustrates the approximate conservation of momentum before and after the perfectly inelastic collision, (P_final-P_init)/P_init = -0.02, and the substantial loss of kinetic energy, (K.E._final-K.E._init)/K.E._init = -0.52. The latter result compares well with that expected in a completely inelastic collision, (K.E._final-K.E._init)/K.E._init = -m₂/(m₁ + m₂) = -0.5.