Physics 111 Lab #8:
Simple Harmonic Motion
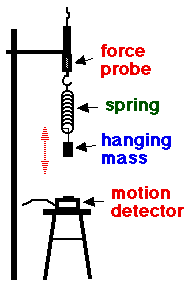
A force probe and motion detector, in conjunction with an oscillating hanging mass on a spring, will be used to study simple harmonic motion (Lectures
24,
25).
Key Activities:
Simple Harmonic Motion
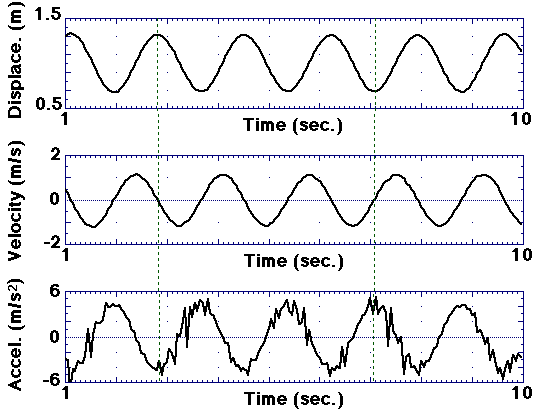
One activity will involve studying the displacement, velocity, and acceleration of a mass experiencing simple harmonic motion (Lectures
24,
25).
What's happening?
Dependence of the Oscillatory Period on Amplitude
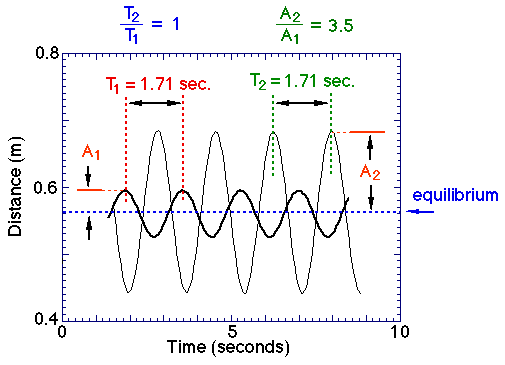
The dependence of the oscillatory period, T, of an object on the amplitude of the oscillation during simple harmonic motion will be studied. The results shown here illustrate the independence of oscillatory period on amplitude (Lectures
24,
25).
Dependence of the Oscillatory Period on the Spring Constant
Also, the dependence of the oscillatory period, T, on the spring constant, k, will be studied during simple harmonic motion. A "best fit" to the data shown here exhibits the expected T ~ k-1/2 dependence (Lectures
24,
25).
What's happening?
Dependence of the Oscillatory Period on Mass
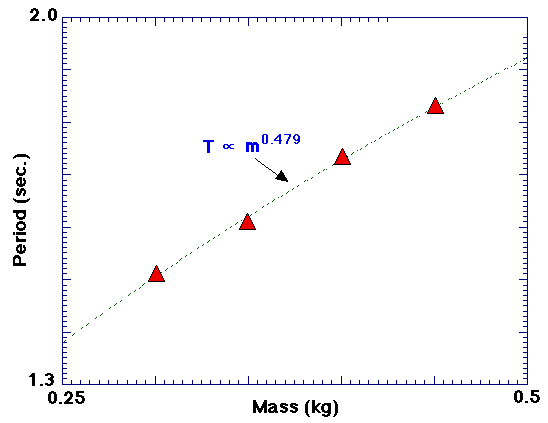
Finally, the dependence of the oscillatory period, T,
on the mass, m, of the object will also be studied. A "best fit" to the
data shown here is quite close to the expected T ~ m1/2 dependence
(Lectures
24,
25).
What's happening?
Energetics of Simple Harmonic Motion
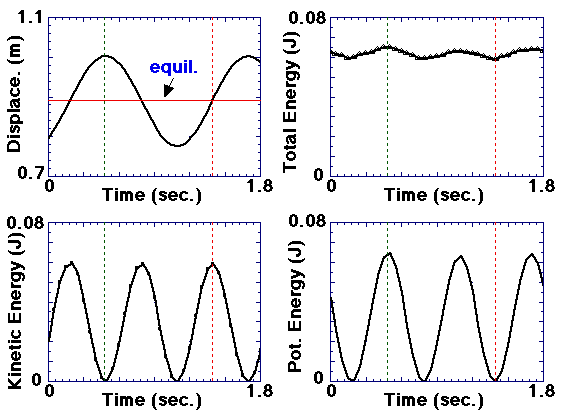
The energetics of an object experiencing simple harmonic
motion will also be studied in order to demonstrate both the relationship
between potential and translational kinetic energies, and conservation of
energy in the absence of dissipation (Lectures
24,
25).
What's happening?
Damped Harmonic Motion
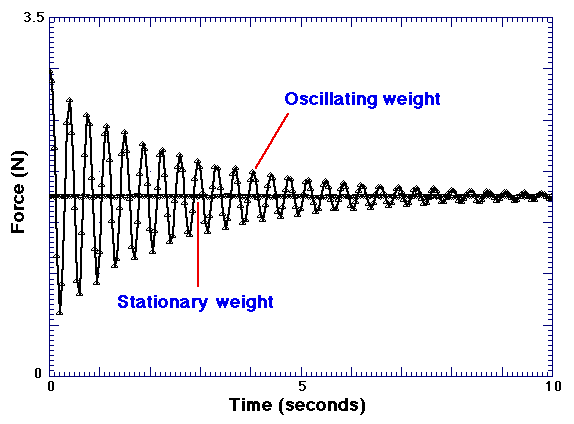
Finally, the effects of damping on simple harmonic motion will be investigated and analyzed. The graph to the right shows the force exerted on the force probe by a mass hanging from a rubber band. The damping in this case is rather large.
This activity will focus on the displacement and energy loss exhibited by the mass+spring system illustrated at the top of the page. Both the displacement and total energy of the mass exhibit the characteristics of damped oscillatory motion, as shown here. Notice in particular that the energy shows a clear exponential decrease with time, E(t) = Einite-bt/m, where b is the damping constant, m is the hanging mass, and Einit is the initial total energy of the mass+spring system.
What's happening?
Last (Lab #7)
Next (Lab #9)
Lab Page
Show me the Prelab
Back to Lab Page