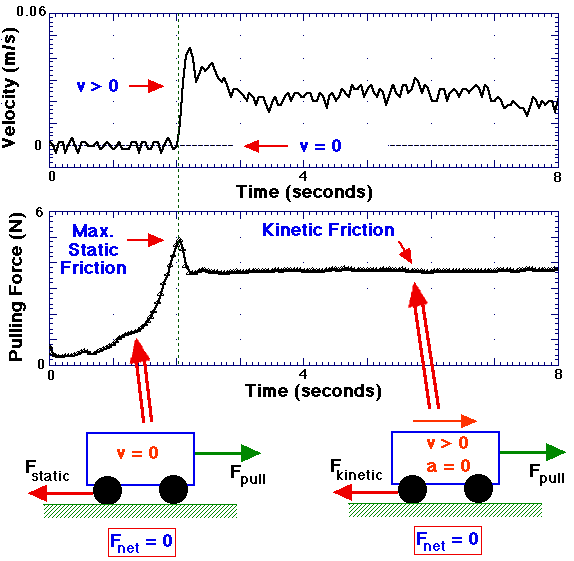
Initially, the static frictional force, Fs,
increases so as to maintain a magnitude equal to, and a direction opposite,
the pulling force. In this regime the net force on the cart is zero and
the cart remains stationary (v=0). However, once the pulling force
exceeds the maximum possible value of the static frictional force,
Fs = µsmg (where µs is the
coefficient of static friction, m is the cart mass, and g is the
gravitational acceleration), static friction can no longer balance the
pulling force, and the cart starts to slide. The pulling force necessary
to maintain a constant cart velocity (net force = 0) beyond this point
has a magnitude equal to (and a direction opposite) that of the kinetic
frictional force, Fk = µkmg. Since
Fk<Fs (µk<µs),
the magnitude of the pulling force in this regime is less than the maximum
magnitude of static friction (Lecture 7).
