Damped Harmonic Motion
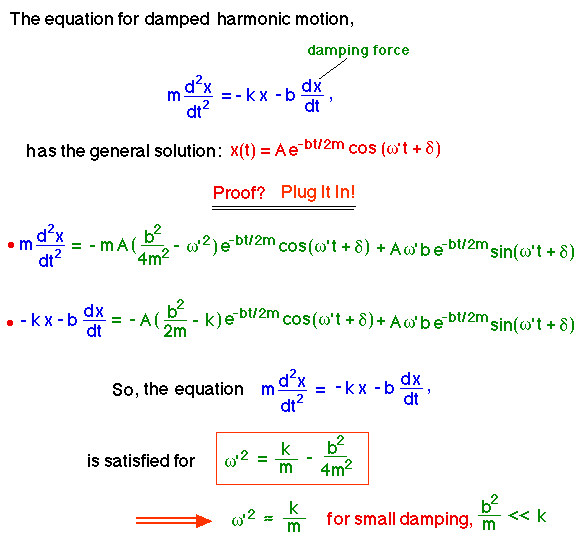
If a velocity-dependent damping term is added to the simple harmonic motion equation in order to account for frictional effects, the resulting displacement is predicted to have an oscillatory behavior with an amplitude that decreases exponentially. Notice that in the case of a small damping constant, b, the oscillatory frequency of a damped harmonic oscillator is predicted to be approximately the same as that of the undamped harmonic oscillator.
Energy Loss in a Damped Harmonic Oscillator
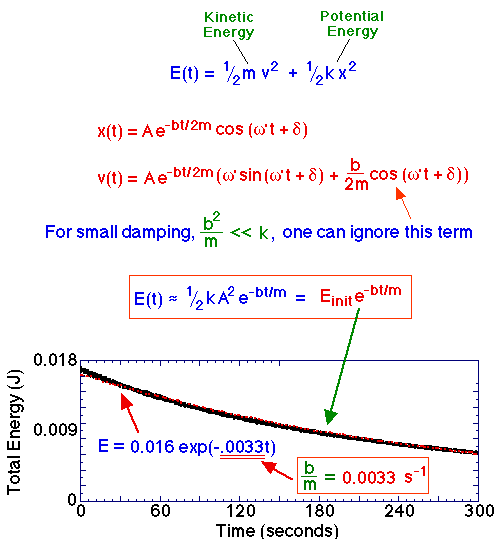
As shown here, the total energy of the damped harmonic oscillator in this activity can be nicely fit by the following theoretical expression for the energy of a harmonic oscillator with small damping: E(t)=Einite-bt/m, where b is the damping constant, m is the hanging mass, and Einit is the initial energy.
Back to Lab #8