UIUC Physics 406
Acoustical Physics of Music
Electric Guitar Pickup Measurements
We have developed a PC-based DAQ system that enables us to measure the complex impedance Z(f) = V(f)/I(f) of electric guitar and bass
pickups. A PC talks to an Agilent 33220A function generator via GPIB (General Purpose Instrumentation Bus) controlling
its frequency (nominally 5 Hz to 20.005 KHz in 10 Hz steps) and voltage amplitude (nominally 1.0 volt).
The sine-wave signal from the function generator (a near-ideal voltage source, 50 Ohm output impedance) is
converted to a near-ideal constant current source, simply by sending the signal through a 1.5 meg-ohm metal film resistor.
The sinusoidal signal after the 1.5 M resistor is connected to the electric guitar pickup. A 100 Ohm metal film resistor
is connected in series with the pickup on the ground side. The voltage across the pickup and current flowing through the pickup
(measured as a voltage developed across the 100 Ohm resistor in series with the pickup) are first buffered by low-noise, unity-gain
precision instrumentation op-amps (AD624's), the voltage signals of which are input to SRS830 DSP lock-in amplifiers.
We record the in-phase ("real") and 90-degrees out-of-phase ("imaginary"/quadrature) components of the complex voltage V(f) and current I(f) output
from the SRS830 DSP lock-in amplifiers {both of which are phase-referenced to the sinusoidal signal output from the function generator}.
Four 12-bit ADC's (Analog-to-Digital Converters) on a National Instruments LabPC+ DAQ card are used to digitize the
in-phase and 90-degrees out-of-phase signals output from the two lock-in amplifiers: Re(V), Im(V), Re(I), Im(I).
We then compute, on-line (and off-line) the magnitudes and phases of the voltage and current, |V| and |I|, and phi_V and phi_I respectively.
We also compute, on-line (and off-line), the in-phase, 90-degrees out-of-phase components, and magnitude and phase of the complex impedance Z(f) = V(f)/I(f),
i.e. Re(Z), Im(Z), |Z| and phi_Z at each frequency, f as well as those parameters associated with the complex electrical power
{P(f) = V(f)I*(f)}, i.e. Re(P), Im(P), |P| and phi_P at each frequency, f.
We also measure the DC resistance of the guitar pickup, Rdc using a Fluke 77 DMM (Digital Multi-Meter).
We measure the Inductance L(f) and so-called Dissipation, D(f) at 120 Hz, 1.0 KHz and 10.0 KHz (when possible)
using a Hewlett-Packard LCR meter {note which simply analyses the pickup as either a series or parallel L-R circuit}.
We measure the polarity of the magnet poles (north or south) at the top of the pickup, using a simple compass and/or a Hall probe.
We record the type of permanet magnets used in the pickup and measure the strength of the magnetic field, B at the top of each of
pole screws/slugs in the pickup, using a Hall probe. We record the winding direction/sense of the pickup coil (CW/CCW)
viewed from the top of the pickup (where possible).
A pix of the Electric Guitar Pickup Test Stand in the UIUC Physics 498POM Lab:

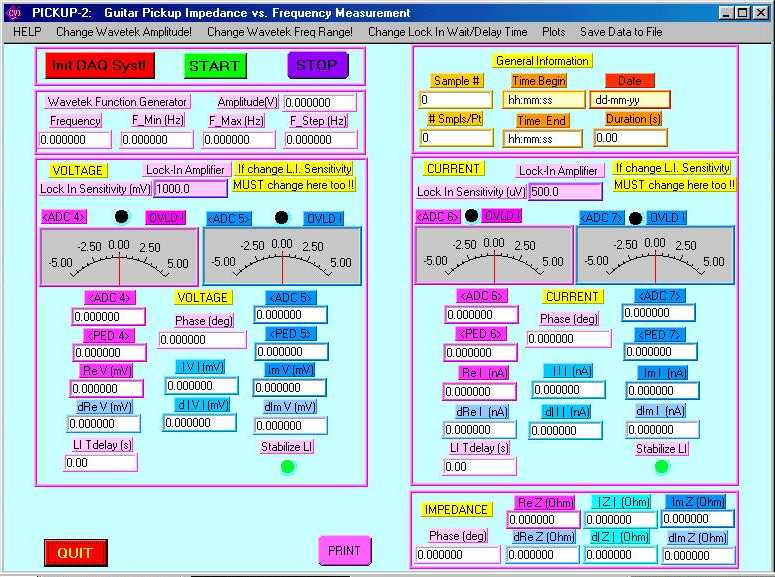
Here is a pix of main display panel for the Electric Guitar Pickup DAQ setup in the P498POM Lab:
The following document summarizes the various methods and equipment we use
to obtain the various physical measurements that we make on various electric
guitar, electric mandolin and bass guitar pickups, and the definitions and
conventions that we use for the various quantities that we measure.
The following is a Microsoft Excel file that summarizes the various physical measurements
we have made for various electric guitar, electric mandolin and bass guitar pickups.
Dan Carson, a UIUC Physics senior, worked with Prof. Errede during the Spring, Summer and Fall Semesters, 2009
investigating the electromagnetic and condensed-matter properties of electric guitar pickups for his Senior Thesis.
We developed a MATLAB-based least-squares fitting program to extract the {lumped} inductance L(f), capacitance C(f),
and two AC resistances Rl(f) and Rc(f) as well as the inductive and capacitive stored energies,
Wl(f) = 1/2L(f)I(f)**2 and Wc(f) = 1/2C(f)V(f)**2 vs. frequency, f.
We show (here) the measurements of complex voltage V(f), current I(f), impedance Z(f) = V(f)/I(f) and power P(f) = V(f)I*(f) vs. frequency, f
e.g. for a 1952 Gibson BR-9 Lap Steel P90 pickup, obtained with our PC-based Electric Guitar Pickup Impedance Measurement DAQ System.
We wrote a MATLAB-based least-squares fitting program to analyze the complex V(f), I(f), Z(f) and P(f) vs. frequency, f
electric guitar pickup data to extract the {lumped} inductance L(f), capacitance C(f), and two AC resistances Rl(f) and Rc(f)
as well as the inductive and capacitive stored energies, Wl(f) = 1/2L(f)I(f)**2 and Wc(f) = 1/2C(f)V(f)**2 vs. frequency, f.
{Note that the DC resistance of the pickup, Rdc is a fixed parameter (i.e. a constant).}
These LSQ fit results, associated with the above 1952 Gibson BR-9 Lap Steel P90 pickup are also contained in these files.
P90-style pickups are interest here because they can be {non-destructively} taken apart, enabling the study of how these
{lumped} parameters change as the pickup is put back together, one piece at a time!
Comparison plots of {lumped} inductance L(f), capacitance C(f), and two AC resistances Rl(f) and Rc(f) for
[1] bare coil +coax cable only, [2] coil +coax cable + magnetic permeable materials, [3] coil + coax cable + magnetic permeable materials + magnets, [4] complete pickup assembly associated with the above '52 Gibson BR-9 Lap Steel P90 pickup.
The following sequence of plots show the effect(s) of loading e.g. the '52 Gibson BR-9 P90 pickup by its volume/tone controls and a guitar cable.
Loading a guitar pickup just with e.g. a 500 K resistor (i.e. the volume control) *dramatically* increases the width of the resonance,
as well as decreases its peak height. Additionally loading the pickup e.g. with 500K tone control + tone control cap {to ground} tosses signal
away in a frequency-dependent manner, since the tone control is a simple R-C first-order, passive low pass filter network.
Additionally loading the pickup + volume/tone controls with a 20' guitar cable (~ 60 pF/foot of capacitance) adds ~ 1200 pF of
capacitance to the pickup, resulting in shifting the resonant peak, fo of the pickup {since fo ~ 1/sqrt(LC)} and reducing its output.
7/7/2009:
We have been measuring the electromagnetic properties of hundreds of different types of electric guitar pickups over the past ten-twelve years;
we will be posting the results of some more of these pickups in the near future, as we turn the crank on this LSQ fit pickup analysis program....
 Return to the UIUC Physics 406 Experimental Results Page
Return to the UIUC Physics 406 Experimental Results Page
 Return to the UIUC Physics 406 EMI Sub-Webpage
Return to the UIUC Physics 406 EMI Sub-Webpage
 Return to the UIUC Physics 406 Home Page
Return to the UIUC Physics 406 Home Page
