Topics:

 

Next time:

 

Some key searches for the aether

 

The problem raised by Maxwell's equations is that the velocity of electromagnetic waves does not seem to change. It is fixed. This violates Galillean invariance. Initially it was thought that there was something wrong with Maxwell's equations. This turned out not to be true. The next suggestion is that Maxwell's equations are valid in some preferred reference frame--some absolute reference frame. This absolute reference frame was called the aether. Here are the three tests of this hypothesis.

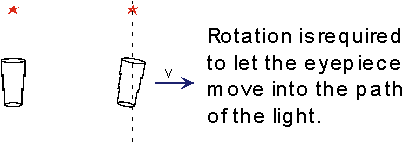
If the telescope (mounted on the earth) moves through the ether, you have to tilt the scope a little so that the rear end is in the right place when the light gets to it. As the Earth goes around the sun, the apparent direction of a star changes by ±0.3 minutes of arc. This is only x10 smaller than Tycho could see by eye, and is easily measured with a telescope.

Conclusion: The Earth changes its motion through the ether periodically, just as it's supposed to if it orbits a Sun which is not accelerating.

(Proof of Copernicus’ theory?) (Proof of ether idea?)

But since we don't independently know which is the "true" position of the stars, we don't know at what time our telescope is pointed straight at the stars and when it's tilted. We've measured that the Earth's velocity changes, i.e. the earth has an acceleration, but we have not yet accessed its velocity relative to the ether.

 

• Ether drag . It was known that light moves more slowly through materials which have an index of refraction.

Fizeau's experiment

Fizeau measured the velocity of light in water under three circumstances: 1) static water, 2) water moving in the direction of the light, and 3) water flowing against the light. He observed that the speed of light was faster when the water moved in the direction of the light than when it flows counter to the light. Conclusion: the water drags the aether along for the ride. This helped confirm the aether hypothesis.

But we still haven't managed to measure the Earth's speed- here we just measured the change in velocity of the speed of light depending on the direction the water is flowing.

 

Something is frustrating: we have all sorts of experiments that fit a theory that says that Maxwell's equations only work in a special frame- but somehow we can't quite measure our motion with respect to that frame.

The time was ripe for a more serious experiment to measure the absolute motion of the Earth.

We need light just propagating in a vacuum, not any of these messy complications due to interactions with moving matter. And we need a round-trip, so that we can compare timing of two signals at the same place.

Michelson-Morley Experiment: Null Result

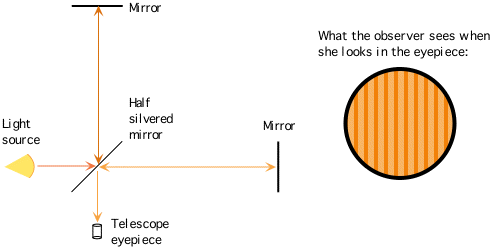
Michelson and Morley oriented the apparatus so that the initial line of propagation of the light was nearly along the earth's motion in its orbit at a certain time in the day. The orbital speed is 18m/s. The aether speed should be at least this amount. If light propagated on the aether, then the velocity of light in the direction of motion of the apparatus should be different from that in the direction perpendicular to it. This is a very sensitive method, because the wavelength of light is 5´ 10-7 meters. The experiment was supposed to be sensitive enough to detect the rotation of the Earth (30 km/s) as well as the orbital motion. No effect was noticed. That is, the speed of light was the same in the direction of motion of the apparatus as well as perpendicular to the apparatus. This would imply that the aether speed is zero. Or??.

Possible explanations:

 

Lorentz-Fitzgerald Contraction (1892)

 

In order for the third explanation to work, the contraction must exactly cancel the expected effect. In technical terms, "a conspiracy." The size of the effect is tiny:

For v = 30 km/s the factor is ~0.999999995 (i.e., 1 - 5´10-9).

Did this make sense? Maybe, because materials are held together by chemical (electrical) forces, so the same thing that affects light might affect materials as well. However, there was no quantitative theory that predicted the contraction.

To maintain a consistent picture, clocks which are moving through the ether must also run slowly by the same factor (time dilation). Lorentz also found that it seemed necessary for masses to change as they moved through the ether.

These two effects are part of what is called the Lorentz transformation. They are important features of special relativity.

 

"Almost" Relativity?

In 1904, Poincaré suggested that it might be impossible to measure one’s speed through the ether. He proposed that "A complete conspiracy is itself a law of nature." He asked, "What must be true if one’s speed through the ether is to be unobservable?" He was able to show that the mass of an object (the "m" in momentum = mv) would increase as an object’s speed increased. Also, the speed of light would be the maximum possible speed.

These conclusions may sound familiar to those of you familiar with Special Relativity.

However, there was still an underlying assumption (left over from the first impression made by Maxwell's equations, and perhaps from our Aristotelian instincts) that one reference frame was "right", however hidden it might be.

 

So will the special aether frame ultimately reveal itself or not?

"The principle of physical relativity is an experimental fact ... and as such it is susceptible to constant revision." "The principle of relativity thus does not appear to have the rigorous validity which one was tempted to attribute to it."
Poincaré,quoted by Holton, p. 205.

 

The situation was unsatisfying from a philosophical point of view to Lorentz and Poincaré and others:

"...surely this course of inventing special hypotheses for each new experimental result is somewhat artificial. It would be more satisfactory if it were possible to show by means of certain fundamental assumptions ..."
H.A. Lorentz, quoted by Holton, Thematic Origins of Scientific Thought, p.229.

 

Maybe the principle of relativity should be taken as a postulate, not just a contingent fact. (At least tentatively.)

Will that give us anything beyond the description of the phenomena in terms of Lorentz contraction, time dilation, etc.?

Einstein's approach: initially motivated by Mach’s conception of a completely relationist universe. (For Mach, even acceleration was relative.) Precursors to special relativity retained the notion of absolute space in the guise of the ether. This was unsatisfying to Einstein, even though for Poincaré, the ether had become as undetectable as Newton’s absolute space.

 

"It is known that Maxwell’s electrodynamics – as usually understood at the present time – when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. " Einstein, "On the Electrodynamics of Moving Bodies, Annalen der Physik, 17 (1905).

Einstein:

"The phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest. The same laws ... will be valid for all frames of reference."

That postulate (relativity) sounds familiar, but how can we combine it with Maxwell's equations?

 

Einstein’s two Postulates

1 "If, relative to K, K’ is a uniformly moving coordinate system devoid of rotation, then natural phenomena run their course with respect to K’ according to the same general laws as with respect to K. This statement is called the principle of relativity (in the restricted sense)." Einstein, Relativity, p. 16.

This principle applies to all phenomena (including electrical and optical), not merely mechanical.

So, what to do about Maxwell’s equations? We accept them:

2 "... experience in this domain leads conclusively to a theory of electromagnetic phenomena, of which the law of constancy of the velocity of light in vacuo is a necessary consequence." p. 23.

The insistence that these two "apparently incompatible" principles are consistent is the new idea.

Let's see if we can make sense of these two statements. Einstein took the results of the Michelson- Morley experiment to be a fact of the world. It is a law that the speed of light is independent of the uniform motion of an observer. But if this is true, how can different observers see the same laws of nature are holding in their respective reference frames. Let's make this clearer. We know from Galileo that if two objects are in motion relative to one another, then the velocity that they see is related to the difference or the sum of their velocities depending on whether the two objects are moving towards one another or away from one another. Let's assume we are travelling with a velocity u towards a light source. On the Galilean account, we would expect to measure that the light beam is moving at a velocity of c-v. But Einstein tells us that this is not the case. We instead see that the light speed is c not c-v. That is, our velocity does not matter. So we expected a smaller number than what Einstein tells us is the case. How do we reconcile this. Speed is length/time. A simple way to reconcile this is to say that the time increment that we are experiencing is actually shorter as a result of our motion. That is, time is slowing down for us as we move. Let's make this more concrete. Let's assume that we are moving with velocity v. Once we get to point A, a light bulb is turned on. We then measure the time for the light to move to another point B immediately ahead of us. Let us say that on the ground the distance between A and B is L. Then the speed of light is simply c=L/t, where t is the time for the light to travel from A to B in the stationary reference frame. Now what about our moving frame. In our moving frame, we see the light reach B at some time t' which is shorter than t. However, the speed of light that we measure must be the same. Hence, the length that we measure to be the distance between A and B must be different from L. Let us call this length L'. In the moving frame, we have that c=L'/t'=L/t. If we solve this equation for L', we find that L'=L(t'/t). Because (t'/t)<1, we measure that L' is less than L. That is, in the moving frame, lengths are contracted. Hence, the constancy of the speed of light tells us two profound things: lengths contract and time is dilated upon uniform translation. These results follow from the simple law of the constancy of the speed of light. Time dilation is derived explicitly below.

 

  • Time Dilation

    • We immediately derive that two observers (moving w.r.t. each other) cannot agree about time intervals.

    The first thing we must do is define what a clock is. A clock is an object which repeats a process many times in succession. A clock "ticks." A simple clock might be a pair of mirrors with a pulse of light bouncing back and forth. Three "snapshots":

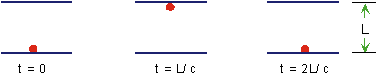
    Consider what happens when two identical clocks are moving w.r.t each other. Look at the path the light travels:


     

    K says that the moving clock ticks slowly by a factor of , because the light travels farther between bounces, but it is moving the same speed.

     

    But how did we know that the width of ticks of the moving clock are the same in both reference frames, what with all sorts of things changing?

     


     

    Lengths perpendicular to the motion remain unchanged. That is, moving observers agree about the dimensions of objects along directions transverse to the relative motion. Can you figure out why?

    A B A B

     

     

     

     

    If the moving rod either shrinks or grows, that determines which rod leaves scratches on the inside of the other. But by symmetry, it has to go the other way as well. Anybody can come by at any later time and see who actually got scratched. So it's an objective feature, and everybody has to agree how it came out. By symmetry, the two lengths must then be the same in either frame.

    Notice that the argument implicitly assumes that some features of the observed world must be invariant.