Topics
: The new invariants
Next
:
The unification of electricity and magnetism
Einsteinís one simple postulate solves a lot of problems.
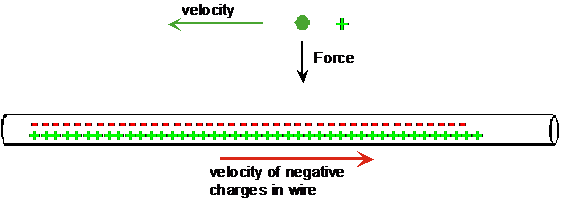
Consider the magnetic force on a moving charge due to the electric current in an electrically neutral wire (no electric field): 
The magnetic force occurs when the charge is moving. If we look at it from the chargeís point of view
(i.e., in its own "rest frame"), there canít be a magnetic force, but there must be some kind of force, because the charge is accelerating.So, the principle of relativity tells us that the charge must see an electric field in its rest frame.
(Why must it be an electric field?) How can that be? The answer comes from Lorentz contraction. The distances between the + and - charges in the wire are Lorentz contracted by different amounts because they have different velocities. The wire appears to have an electrical charge density. (The net charge in a current loop will still be zero, but the opposite charge is found on the distant part of the loop, where the current flows the opposite direction.)When we change reference frames, electric fields partially become magnetic fields, and vice versa. Thus, they are merely different manifestations of the same phenomenon, called electromagnetism.
The first oddity of Maxwell's equations was that the magnetic force existed between MOVING charges. But now we say that there's no absolute definition of MOVING.
The resolution is that whether the force between two objects is called electric or magnetic is also not invariant.
(Neither is the exact magnitude of the force, but that's another problem.)
What happens to the momentum of an object losing energy?
Consider a star, with two blackened tubes pointing out opposite directions. Light escapes out the tubes, but only if it goes straight out. It carries momentum and energy, known (by Maxwell) to obey E=pc.
In order for the light to get out of the moving tubes without hitting the edges, it must be going forward a bit (angle v/c)
So net forward momentum is lost to the light. The lost momentum is: (v/c)
DE/c, where DE is the lost energy.If we assume that total momentum is conserved:
v(
Dm) +(Dv) m = (v/c2) DE.So we can figure out a relation between the lost mass and the lost energy, if only somehow we can figure out how much the star's velocity is dropping, i.e. what's
Dv?
The one thing you know easily is
Dv = 0, because our choosing some reference frame with v Ļ 0 can't make the star accelerate.There is no preferred reference frame: we mean it and we use it all the time in calculations.
So the
Dv drops out of the equationv(
Dm) +(Dv) m = (v/c2) DE.giving:
Dm = DE/c2A reasonable extrapolation is to drop the delta:
m = E/c2
This does NOT say that "mass is convertible to energy". It says that mass and energy are two different words for the same thing, measured in units that differ by a factor of c2
.A word on this equation. The mass appearing in this equation is the same mass that appears in the equation p=mv. We take it as a definition that m is the constant of proportionality between the momentum and the velocity. If this is true, then m=m_0*time dilation factor (1/sqrt(1-v^2/c^2)). m_0 is called the rest mass and m the relativistic mass. If we accept this definition, then we have to give up on F=ma. It turns out the mass in this equation will depend on the direction. That is, mass must be thought of as a vector if we use Newton's second law. There are two main conventions in physics: 1) m=m_0*time dilation factor and 2) m is an invariant given by m^2=(E^2-(pc)^2)/c^2. The high energy physicists use the latter and everybody uses the former. It does not matter which one you use. Just be consistent.
So on the first account mass is not an invariant. Is there anything "real" about an object, i.e. not dependent on how you look at it?
Old invariant:
mNew invariant:
E2-p2c2= m02c4
Photons have no rest mass
Then how can they have momentum? We cannot really understand this until we introduce quantum mechanics. However, let's imagine an object which has E/c = p. Then, (E/c)
2 - p2 = 0. Does this mean that this object has no invariant mass? Is this possible?Yes. Light has this property. One can measure E and p for light and verify that this relationship holds.
The 4-dimensionality of SR requires that any object moving at the speed of light have this property. (I wonít prove it here.) This is an important result.
What does "mass" mean?

I can measure the energy and momentum of the stuff inside by letting the box collide with other objects (assume the box itself to be very light so we can ignore its energy and momentum). Suppose that when the box is at rest (p=0), I measure energy E
o. Therefore, the rest mass of the stuff is given by 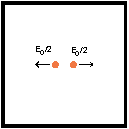
The rest mass of a collection of objects does
not quite equal the sum of their individual rest masses.
Now ask a related question
:If one measures the mass of an atom without knowing anything about its internal structure, how is one to know what it is really made of?
Newtonís concept of mass as "quantity of matter" is gone. It has been replaced by a Lorentz invariant relationship between energy and momentum.
The reason why Nís concept works so well is, as usual, that unless we are dealing with objects moving at or near the speed of light, the effects are tiny. For example, in a macroscopic object at room temperature, the extra mass due to the thermal energy (in SR, all energy contributes to mass) is about 10-10 of the mass of the atoms. Thatís why Newton was able to assume conservation of mass.
In the Newtonian limit, mass does tell us "the quantity of matter" (i.e., the total number of protons and neutrons), but this is only an approximation.
4-dimensional spacetime
Three-dimensional geometry becomes a chapter in four-dimensional physics. ... Space and time are to fade away into the shadows.
In 1908, Minkowski realized that there is a beautiful
geometrical interpretation of SR. It is based on the mathematical similarity between rotations and Lorentz transformations. However, you need not stick to this presentation. By far the simplest presentation is that of Rohrlich's on pages 76-86. In fact, this is what I will present in class.Geometrical Interpretation
In the geometrical interpretation of SR, thatís what c is. Itís the number of meters per second, just a conversion factor.
The geometrical interpretation of SR helped lead Einstein to general relativity.
This is a prime example of the value of theories beyond explaining old phenomena and predicting new ones. Mathematically equivalent ways of describing phenomena aren't always psychologically equivalent, they can lead to different types of new theories.
What has really happened philosophically?
The old invariants (t, lengths, m Ö) (things which were "real" in that they were observer-independent) have been tossed out. They are replaced with new invariants (c, d2-c2t2, E2-c2p2Ö) which have a slightly more complicated relation to our customary observations.
If we had evolved experiencing many relative speeds close to c, there would be absolutely nothing philosophically exotic or particularly "relativistic" about "relativity". The Lorentz transformations would make sense to that hypothetical us in the same way that the Galilean transformations make sense to the actual us. We would just have a different set of invariants. That's why Einstein wanted to name the theory "Invariants theory."
The philosophical excitement comes from the transformation from one theory to the other- ideas that seemed immutable turned out to be mutable
, and there's a lesson to be learned from that process.
World lines
In barest terms, the history of an object consists of a graph of position versus time, called a world line:
If an object is at rest in any inertial reference frame,
its speed is less than c in every reference frame.
Causality in SR
The speed limit divides the spacetime diagram into causally distinct regions.

Consider events A, B, C, & D. A might be a cause of B, because effects produced by A can propagate to B. They cannot get to D without travelling faster than light, nor to C because it occurs before A.
Similarly, C might be a cause of A, B, and/or D. D could be a cause of B, because light can get from D to B (they lie on a 45į line).
We can determine possible causal connections by evaluating the interval, (ct)
2 - x2, separating pairs of events. If the interval is positive, then a causal connection is possible. This is known as a "timelike" interval. If it is negative ("spacelike") then no causal connection is possible.
Causality in Special relativity:
Strong form: No event can be affected in any way by events outside its past light cone. This applies to conversation laws as well.
Weak form: No information may be transmitted except forward within a light cone.
Weaker form: No information can be transmitted except within a light cone.
You may wonder why we make such pointless distinctions. Can't any "effect" be used to transmit information? Stay tuned.
In a deterministic world, The Strong form would mean that an event would be completely predictable on the basis of knowledge of its past cone alone. Observations OUTSIDE the past light cone might provide the same info in more convenient form, but would never be needed, because everything knowable about the event would be determined by the preceding events in the light cone.
What about in a world where things are not completely predictable on the basis of anything? The Strong form would mean that one could find within the past light cone enough information to obtain a much predictive accuracy as possible about an event.
When we say "Nothing can travel faster than the speed of light", what do we mean?
(What happens if you can send info backward? Say you send your grandma info that somebody much cuter than your grandpa was about to move into her neighborhood. Then you aren't born. Then the info doesn't get sent. So you are born, so ÖÖ.)
If "no object travels faster than c", then the following aren't objects:
The crest of an E-M wave in matter. (Certain materials have index of refraction less than 1 over some frequency range, hence a "phase velocity" greater than c for some light.)
The bright spot made by a beacon shining on a wall.
The cutting point of a scissors.
What are we then claiming?
If we are to describe the world as having some primary constituents, with various higher-level phenomena just being patterns in the constituents' behavior, we want to restrict the primary constituents to those which don't travel faster than light. We claim there exists SOME complete description of the world in terms of constituents which don't travel faster than c.