
Topics
:Next
:
Aside from its profound experimental consequences (length contractions and time dilation), special relativity is important because it establishes the fundamental invariance principle that ties together the Newtonian world and that of Maxwell. The key principle is that uniform motion does not change the laws of physics and hence must leave both theories unchanged.
An important consequence of the principle of relativity is that if the laws of physics are to be the same in every inertial reference frame, the quantities on both sides of the = sign must undergo the same Lorentz transformation (xa=xb
® xa’=xb').Consider momentum. In Newtonian physics, p=mv
(bold means vector). Momentum and velocity are vectors, and mass is a scalar (invariant) under 3-d rotations. This equation is valid even when we rotate our coordinates, because both sides of the equation are vectors.We want to generalize this to 4-d. The natural (and correct) answer is that momentum is a 4-d vector
(4-vector for short). That is, in addition to the x, y, and z components that it used to have, momentum now has a "t" component as well. The fourth component of momentum is E/c, the energy. The factor of c is needed to give it the same units as momentum.Just as the lengths of 3-vectors remain unchanged under rotations, there is an invariant "length" of 4-vectors under Lorentz transformations. The length
2 of a 4-vector is the square of its time component minus the square of its space component: (E/c)2 - p2 = (m0c2)2Notice that you cannot make any invariant from space or time variables alone. That's why we call the SR world is 4-D, and call the old world 3-D + time. No true feature of the world itself is representable in the 3 spatial dimensions or the 1 time dimension separately.
The Replacement of Newtonian Space & Time
by an Ensemble of Meter Sticks and Clocks

The establishment of a coordinate system for measuring position and time is done by distributing a set of clocks on a lattice. Clock synchronization is done by sending a round trip signal between two clocks. The signal is assumed to arrive at the second clock halfway between emission and reception by the first.
The position of each clock is measured similarly. Half of the round trip time, divided by c, gives the distance.
Why so complicated a specification? There is no absolute space or time to rely on, so we need an alternative. Without
an operational definition of position and time measurements, it would be difficult to understand the odd effects that we’ll encounter.
Einstein's operational recipe (make a bunch of identical rods and clocks, build a lattice of the rods to mount the clocks on, check the clock synchrony with light rays) also allows you to check if relativity is correct. It assumes that once the clocks are synchronized by this procedure, they will stay synchronized. (It also makes other assumptions, but we needn't think about them.)
So while you are getting used to the ideas that:
Einstein has at least opened the possibility that his Special Relativity also is wrong, there may be no inertial frames.
Motivation for General Relativity
Special relativity applies to inertial reference frames, that is frames that are not accelerating. Hence, it does not apply to frames in which gravity is acting. Einstein hunted for the general theory that should apply when gravity was present. The first problem Einstein had to solve was gravity, namely how do we really know that we are being acted on by gravity?
How do you feel gravity?
The principle of equivalence
"The gravitational mass of a body is equal to its inertial mass." (p. 73)
What does that mean?
Inertial mass
is the m that appears in p = mv or E = mc2 , or (approximately) F= ma. It tells us how much inertia (resistance to being accelerated) an object has.Gravitational mass
is the m that appears in Newton’s law of gravity: F = GMm/r2. It tells us the strength of the gravitational force between two masses. It has been empirically determined that the two kinds of mass are exactly the same to within a part per trillion (10-12).Notice that when you calculate the acceleration of an object using a = F/m the object's own mass, m DROPS OUT,
a = GM/ r2.
The result is that gravity makes every different type of object accelerate together: the effect of gravity is completely describable classically by an acceleration field, as has been known since Galileo’s time.
That means that you don't feel gravity in the same way that you feel other forces. Since all your parts are accelerating together, gravity creates no strains, tickles no nerves…
However, as Einstein put it, he was the first to "interpret" this fact.
The principle of equivalence
Consider the famous "elevator" gedanken experiment (E called it a chest). We are somewhere in intergalactic space, with no planets or other junk nearby. Fred is resting at ease in his unaccelerated reference frame. Barney, on the other hand is inside a box and can’t see out.
Suppose there is a rope attached to the box, and some external agent pulls on the rope, accelerating the box at exactly 9.8 m/s2.

Fred says
: "The box (and Barney) are accelerating. So what?"Barney says
, "I am not accelerating. I am in an elevator which is hanging from its cable in a gravitational field It's the same field that's making Fred fall, because no cable supports him."Who is correct? Einstein insists that in the absence of a reason for preferring one point of view, one must accept both. This is the strong principle of equivalence, namely that all phenomena are equally describable by either picture. The weak principle of equivalence asserts that the gravitational and inertial masses are the same.
Einstein proposed another modest generalization:
No measurement of any sort can detect a uniform gravitational field.
And no local measurement can detect any gravitational field.
If we accept Einstein's generalization we cannot distinguish an accelerated frame from a gravitational field. We said that no sane person would voluntarily accept accelerated frames, because they lead to all sorts of crazy effects.
If gravity were completely uniform, you could get rid of it by transforming to another reference frame. Gravity can always be eliminated in a small region (e.g., inside Barney’s elevator), but not over a large spacetime domain, because there is an uneven distribution of matter.
So no sane person can reject a universe with gravity: you can't get rid of gravity without getting rid of everything. The gravity isn't uniform.
Observational Consequences
An unexpected consequnce of the equivalence principle is that light rays bend in a gravitational field. Let's just use E=mc^2. The equivalence of mass and energy says that light rays have a mass. Based on the equivalence principle this mass must act like a gravitational mass. Hence, a light ray should fall toward the gravitational source. Note, this means that light is accelerated in a gravitational field. Hence, its velocity is not constant!!!! Waw, this is weird. Didn't we spend alot of time extolling the genius of Enistein and marveling at Michelson and Morley who collectively taught us that the speed of light is constant? It is this apparent contradiction that led to Einstein's theory of general relativity. This theory is much more subtle than special relativity and took much longer to construct. We will see that the answer lies in what we mean by falling in a straight line. General relativity predicts that light rays from a distant star grazing the surface of the sun should be bent by 1.75 seconds of arc. This result is twice that predicted by just using m=E/c^2 and then gravity. Nonetheless it was verified by a total eclipse in 1919. During an eclipse, the light from a star that is just grazing the sun can be seen quite clearly. This should provide a displacement of the star. This displacement was verified in 1919 and heralded the dawn of the Einsteinien world and the demise of Newton. Things would never quite be the same after that. Basically, nothing was left of Newton. Quantum mechanics was just being formulated and that would signal the end of the purely classical interpretaion of what there is.
CONFIRMED, 1919 solar eclipse

Curved-space time
Other strange things happen in uniformly accelerated frames. A light ray travelling at right angles to the acceleration seems to bend, as if it were falling in the direction opposite to the acceleration.
Straight lines are supposed to be the shortest paths between two points. Now the quicker path here IS the path of the uninterrupted light ray (we can see that easily in the LAB frame) but the spatial path length of that light ray seems LONGER than the path of the ray that makes a bounce off the wall. Isn't the speed of light supposed to be constant? If we tried to make our ordinary laws of physics work in such a frame, we couldn't identify light rays' paths with straight lines.
How would we define straight lines?
The path of a light ray? (Doesn't seem satisfactory by our usual standards.)
The shortest path between two points?
(We have to be very careful about how distance is measured)
The locus of a stretched string? (WHEN should the two ends be at particular places, since they don't agree on how fast time is elapsing?)
An abstraction without a simple physical realization?
We'll come back to this question after considering even worse reference frames.
As long as we're looking at yucky reference frames, let's see what would happen if you used a NON-uniformly accelerating reference frame, e.g. a merry-go round.

Before the merry go-round accelerates, you get a bunch of little meter sticks, all stacked together and the same length. If you measure the MGR circumference C and radius R by counting out meter sticks, you find C = 2pR, whether you do this on the MGR or the ground. Now set the MGR spinning. It will stretch, etc, but you tighten down any bolts needed to make its circumference still fall exactly above the previous circumference, traced out on the ground. If you measure on the ground, you get the same old C and R.
Due to the Lorentz contraction, the rulers measuring the circumference on the MGR have shrunk, but not the ones used for the radius. Therefore, in the MGR measurement, C > 2pR. Not only that, the ratio C/R depends on the radius of the circle. (It gets bigger for bigger R.) This is not Euclid's plane geometry, but rather resembles the sorts of geometries you get if you try to confine measurements to curved surfaces. No wonder it's hard to find straight lines with familiar properties!
Geometries in which C/2R
¹ π.Here are 2-d surfaces in 3-d that have each property.
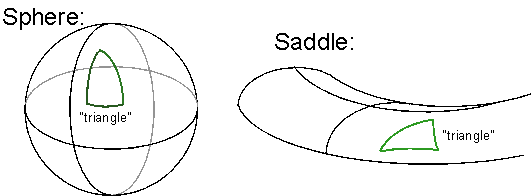
On sphere, C < 2
pR. On saddle, C > 2pR
Other strange things happen:
the sum of the angles of a triangle is not 180°.
If we want to accept non-uniformly accelerated frames as equally valid, we must accept such weird geometry as being the correct description of our 3-d space. In other words, we should be able to distinguish whether we have a non-uniformly accelerated frame by whether measurements confirm Euclid's axioms.
Don't worry about whether the space looks like a piece of some hypothetical Euclidean higher dimensional space, which would have absolutely no physical significance.
We already saw that the outside observers in a rotating frame think that the clocks at the middle are running fast. So if we try to use a rotating frame, clock rates depend on position.
We have a choice:
Obviously, anyone in his or her right mind would make choice (1).
Why then do physicists make choice (2)?
Let me confirm your impression that the answer Is "physicists are mentally defective" by changing the subject to ask a child's question: