Topics

 

Next time

Philosophical implications

Gravitational red shift

Consider a falling object. Its speed increases as it is falling. Hence, if we were to associate a frequency with that object the frequency should increase accordingly as it falls to earth. Because of the equivalence between gravitational and inertial mass, we should observe the same effect for light. So lets shine a light beam from the top of a very tall building. If we can measure the frequency shift as the light beam descends the building, we should be able to discern how gravity affects a falling light beam. This was done by Pound and Rebka in 1960. They shone a light from the top of the Jefferson tower at Harvard and measured the frequency shift. The frequency shift was tiny but in agreement with the theoretical prediction. Consider a light beam that is travelling away from a gravitational field. Its frequency should shift to lower values. This is known as the gravitational red shift of light. This effect should be distinguished from the Doppler red shift of a receding star. We will talk about the latter next class. Any way, the gravitational red shift is a key prediction of the general theory of relativity. 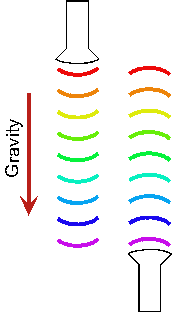In fact, the graviational red shift implies that space is curve. Consider two observers at heights, in a graviational field, as indicated in the figure accompanying this lecture. Lets say the length of the pulse is given by 2\pi N. Let t_bot be the time it takes the sender to send the signal and t_top the time it takes the observer at the top to receive the signal. These times are given by Dt_top=2\pi N/\omega_top and Dt_bot=2\pi N/\omega_bot. From the gravitational red shift, it must be that \omega_topDt_bot. Now consider a space-time diagram in which the height in the gravitational field is the y axis and time is the horizontal axis as shown. Light pulses sent from bottom to top must be sent at 45^o angles. Consider two such pulses. The time delay between the two pulses is t_top and t_bot as indicated. The two light paths must be parallel to one another. However, t_top>t_bot. This is impossible in flat Euclidean space. Hence, space-time must be curved to accomodate a parallelogram in which the two legs are of different lengths but the sides are of equal length. It is not that space is curved separately from time. The only sensible conception is that the union of the two is curved: space-time is curved. (Pound & Rebka, 1960)

Important for devices that rely on high-altitude clocks:

GPS devices positioning would drift off by about 7 miles a day, without GR corrections!

 

Back to the twins: What if Alice doesn't accelerate back toward Earth using rockets, but instead just slings around using gravity from some big planet. She feels no accelerations. So we can't argue anymore that the one who's younger is the one who "feels no accelerations"- neither feels any. Nonetheless, Alice is younger, because she spent time DOWN in the gravitational field of that big planet, so her clocks were all running slow.

You can see G.R. outgrow some of the arguments which led into it.

Gravitational space-warp:

On the merry-go-round, there was missing space inside the circle. Near a star, there should be the opposite effect. A wave passing by the star has to traverse more distance on the part near the star than on the part farther away. The wavefronts farther away get ahead, which turns the wave as if it were being pulled toward the star. That's the extra curvature of light observed in 1919.

 

 

It looks like the wavefronts are closer together near the star, but that's only because I've forced the picture onto this nearly Euclidean page. Really there's extra space there, and all the fronts are equally spaced, as measured locally.

 

 

Note the necessity for an operational definition of distance (and time).

The new equations to describe the gravitational interactions are not the same as Newton's. (Obviously not, since we've now found experimental predictions which differ.) The new equations used to describe how things look from accelerated frames and ones with gravity (i.e. all the frames which exist in the actual world) are called General Relativity.

GR also solved a long-standing problem. Remember way back when we were describing Newton's triumphs?

The orbit of Mercury had been known since about 1800 to deviate from its Newtonian prediction. (The axis of the ellipse rotated, i.e., precessed.) Many unsuccessful searches had been made for objects, such as other planets, that would explain the motion. GR predicts that the orbit of a planet should follow an ellipse that precesses slowly about the sun. Such an orbit is known as the precession of the perihelion. This is a small effect but nonetheless can be measured. In 1845, the precession ofthe perihelion of Mercury was observed. This effect is largest for Mercury because it is closest to the sun. Einstein's GR predicts that the perihelion of Mercury should precess about the sun 43.0 seconds of arc per century. Values of the precession for Venus and Earth are 8.63 and 3.8 seconds of arc per century. The predictions from GR agree with these experimental results within 1%. Hence, this is a key triumph of general relativity.

 

 

 

Some other confirmations of GR : see transparency

Modern versions of the light-deflection experiment:
repeatedly confirmed, now to better than 1% accuracy.

Gravitational slowing of clocks:
repeatedly confirmed, in one case to 0.03% accuracy.

Time-delays are affected by travel near sun:
repeatedly confirmed to within 5% accuracy.

 

Existence of gravitational lenses

Probable existence of black holes

Slowing of pulsar rotation due to gravitational radiation (quantitative)

etc

 

 

Some conceptual implications

 

• Spacetime is beginning to become more substantial than it was (contrary to Einstein’s original motivation). The geometry of spacetime varies from place to place in a way that is observable. We’ll see next time that it’s even more real than this.

• The elevation of unexplained "coincidences" into postulated behavior appears to be a successful strategy.

• Geometry is empirical. Kant was wrong that it was only possible to conceive of the world in Euclidean terms. The world violates Euclid's axioms.

If a good definition of a straight line is "the path followed by an object which experiences no forces" we must recognize:

Gravity is not experienced: in principle a gravitational field cannot be felt locally.

A straight line would then be a path followed by some small object in the presence of no influences other than gravity, i.e. in free fall.

These are called spacetime geodesics

I’m referring to objects moving solely under the influence of gravity (i.e., in "free fall"). This is the non-Euclidean generalization of Newton’s 1st law.

A geodesic is defined to be the shortest line between two points on a surface. In spacetime, this is generalized to be the world line which has the largest interval between two events (4-d points). ("Largest" is an artifact of the - sign.)

 

You may have noticed that on the sphere there are no parallel lines. All geodesics intersect. Similarly, the interpretation of the trajectory of a dropped ball near the Earth is that its world line appears to start out parallel to the Earth’s, but inevitably intersects it.

 

 

Do we need curved spacetime?

Just to be sure it is clear ... The 2-d examples of curved surfaces allow us to look at things from "outside." However, a
2-d person confined to the surface and with no knowledge of the 3rd dimension could still infer the curvature from his own geometrical measurements (e.g., the angles of triangles). That’s the situation we 4-d people find ourselves in. The curvature can be completely defined and all experimental predictions, etc made with no reference to some other dimensions.

The immediate question is do we need curved spacetime, or can we get away with "flat" geometry? (Sklar, 55-67) We have already seen that if we want to put accelerated observers on a par with inertial ones, we need curvature. If we don’t do this, then we need to say that the forces accelerated observers feel are pseudoforces akin to the centrifugal force. Are these two views equivalent?

 

They are equivalent locally (if no singularities), but not globally. Only special configurations of gravity (uniform gravity, for example) can be completely eliminated by going to an accelerated reference frame. In particular, nonuniform gravity gives tidal forces which can’t be transformed away. One can maintain flat geometry if one attributes effects such as the slowing of clocks to dynamics (similar to the pre-SR Lorentz contraction, etc.), but that gains one nothing and is vulnerable to the same criticism (it’s ad hoc) that Einstein made of the pre-SR theories.

If the universe really has the topology of a sphere, that has global consequences (e.g., one might be able to go around) which can’t happen in flat space. (Sklar does not discuss this.) The large scale geometry of the universe is still not known. More on this later. However it is known that the geometry must have at least one singularity- an infinite deviation from the simple flat-space picture, which would be extremely hard to mimic in some fancy flat-space model.

Furthermore, GR makes many detailed predictions which have been beautifully confirmed, and which beat the predictions of a whole slew of rivals- most of which are curved space, anyway. There is no competing theory with the simplicity and predictive power, except theories whose predictions are already known to be wrong.

 

 

 

Is space real?

If GR forces us into non-Euclidean geometry, does this mean that space is "real"? No. A relationist would say that this only implies that the geometrical relations between objects is not what we thought. No substantive spacetime is required.

However, there are two new arguments on the substantivalists’ side.

In GR the gravitational interaction between objects is mediated by the geometry. That is, geometry plays the same role as, e.g., the electric field. An object distorts the geometry in its vicinity. This distortion affects the motion of other objects, because the geodesics are modified. Thus, spacetime plays a more direct role in the dynamics than in Newton’s physics.

Finite propagation speeds give fields more of a reality in SR (and GR) than they had before. We already saw quite dramatically in electromagnetism, in which wave motion of the fields was predicted and then observed. GR makes a similar prediction for the gravitational field. If the Sun were to move we would feel the changed gravity at the Earth 500 seconds later. If the Sun were to shake back and forth, GR says it would emit gravitational radiation (waves) with many of the same properties of EM waves.

If they exist, gravitational waves are as real as any other object. They carry energy and momentum. Only indirect evidence exists at this time (binary pulsar orbits), but detectors are being built to look for them.

The relationist-substantivalist debate is thus a split decision. On one hand, space-time seems to have observable properties in itself, just as much as electromagnetic fields, etc. On the other hand, these properties are far from resembling those expected by those of Newton's space.

Einstein's original motivation was to develop a physics that followed Mach's principle, but GR does NOT follow that principle. (And Mach was unable to follow SR, much less GR.) It may be possible to add Mach's principle as a separate requirement, i.e. to rule out those GR spacetimes which do not obey Mach's principle, but nothing about the structure of GR itself tells you to do so.

 

Newton said that two masses tied together and spun would stretch a string taut, because they would need a force to keep them both accelerating toward the middle, regardless of the condition or existence of anything else. They have "absolute acceleration". Mach said the string could not go taut because "absolute acceleration" is meaningless- you need the other stuff in the universe to create the forces. Einstein abandons the phrase "absolute acceleration", but GR allows solutions in which the string is taut. Such a solution can either be described as two masses rotating in nearly flat space-time OR as a strange twisty space-time exerting peculiar gravitational forces. But operationally, Newton and Einstein agree on what the possibilities are, and they include the possibilities excluded by Mach. GR outgrew its philosophical heritage.