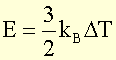
Motivation

We propose to study the motion of two concentric carbon nanotubes and the friction between their walls. Such simulations have not been carried out so far and no experiments has been done to measure the friction. There have been some recent experiments studying the motion of carbon nanotubes on a substrate [4] and studying friction in a system of 8 walled nanotubes [3] so results can be compared with studies of these geometries, but we do not expect our result to exactly match their measurements since our device is not similar to theirs.

Here are a few interesting things we will study about this topic:
 
 

free motion of a double wall nanotube,
motion of a wall when the other is constrained to rotate or to slide,
measurement of the friction coefficient for rotation and sliding,
and the effect of the orientation of the walls.

Preliminary study

We will first study the potential energy of a double wall nanotube when the outer tube is sliding or rotating. By looking at how the potential varies, we will be able to guess what kind of motion could happen on this device.

Molecular dynamics study

First we will look at the free motion of straight nanotubes, straight meaning that the zig-zag axis in parallel to the axis of the tube.

Here are the nanotubes used for this simulation :

- for the inner tube, a [10,10] nanotube with a length of 16 nm long and 6.5 nm of radius.
- for the outer tube, a [15,15] nanotube with a length of 35 nm angtroms and 9.9 nm
of radius.

Next we will see the effect of the orientation of the tube by doing the same simulation to screwed nanotubes.

The nanotubes used for this simulation will be:

- for the inner tube, a [12,8] nanotube with a length of 16 nm angtroms long and 6.5 nm of radius.
- for the outer tube, a [18,12] nanotube with a length of 35 nm and 9.9 nm of radius.

Then we will rotate a wall and probe the motion of the other, we would expect to see a screwing motion of the tube in response.

These simulations will be run at room temperature (300K) in order to facilitate the motions of the tube.

Friction measurement

We will measure the sliding friction by constraining the inner tube to slide and the rotating friction by constraining the outer tube to rotate. We will do these simulations with a screwed nanotube system and with a straight nanotube system. Because we want to prevent any other motion from happening we will run the simulation at the lower temperature of 100K. Because the friction coefficient is expected to be very small (buckyballs are considered as quasi-ideal lubricants) we do no expect to put the system in contact with a heat bath.

Because the constraints constist of moving the outer tube with a given displacement per time-step, we can calculate the elevation of temperature and relate it to a given displacement by knowing the time-step.

The friction energy per atom will be estimated by:

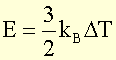
And the energy will correspond to a displacement L:

with
        t= number of time-steps
        f=friction force per atom.
        b=constraints in angtroms/time-step.

Thus, f can be determined by:

We will then have the friction coefficient per atom which can be compared to some experimental data.
 
 

---