The results will constist of a qualitative study of the motion of two concentric nanotubes. We will study a few systems by changing the orientation of the tube and by applying some constraints on the tubes.

Preliminary study of double wall nanotubes without any constrains applied

The preliminary study consists of a molecular statics calculation of the potential of a double wall nanotubes when the outer tube is sliding or rotating. Surface plot of the potential can then be obtained.
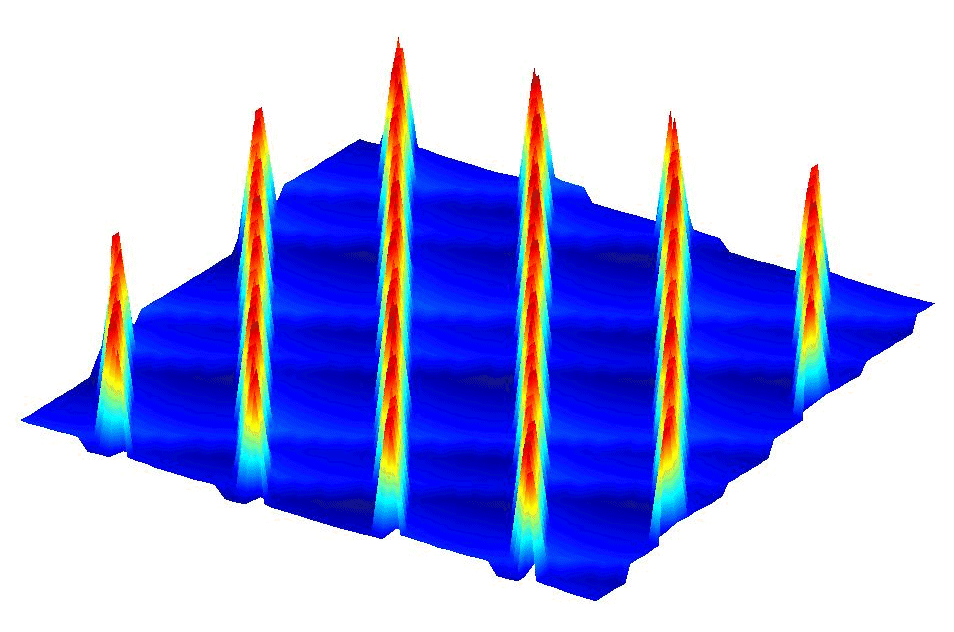
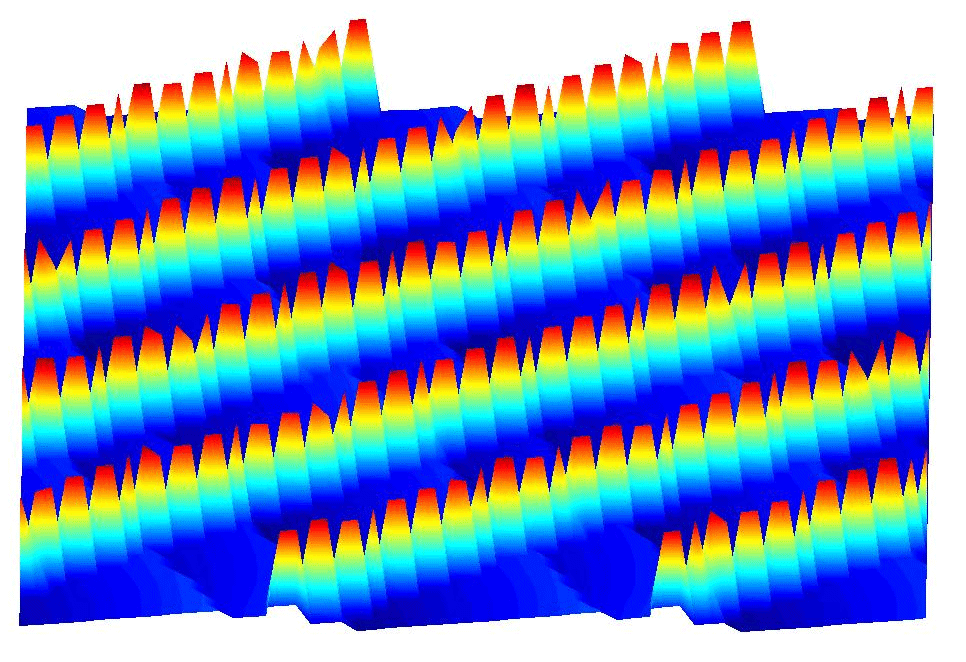
The plots belows show the variation of the potential energy when sliding and moving the outertube. The length scale for sliding and rotating is ranged fron -3 angstroms to 3 angstroms and and the peak heights are typically of 1ev.

The rows of peaks define the rotating direction and the direction perpendicular to the rows represent the sliding direction. We can see that in the sliding direction, the potential is pretty smooth between the peaks. On the contrary, the potential in the rotating direction is composed of many steps.

Qualitative study

Straight double wall nanotubes without any constraints applied (animation)

The temperature of the simulation is 300K and the nanotubes used for this simulation were :
 
- for the inner tube, a [10,10] nanotube with a length of 16 nm long and 6.5 nm of radius.
- for the outer tube, a [15,15] nanotube with a length of 35 nm and 9.9 nm radius.


The simulations of this system show that the only motion of the tubes consists of sporadic sliding of one on the other.  This result is consistent with the preliminary study of the tube by molecular statics. We can see in the 3D map of the potential energy that the potential energy of sliding is defined by a constant energy between peaks. Because no constraints have been applied to the system, the tube is doing a random walk determined by the kinetic energy of the tube. We believe that the range of motion for sliding is wide enough for the tube to have enough kinetic energy to overcome the barrier by moving in between the peaks. Thus, because the potential energy when rotating is not as smooth as when sliding between peaks, there is no rotation of a tube on the other.
 
 

The temperature of the simulation is 300K and the nanotubes used for this simulation were :
 
- for the inner tube, a [12,8] nanotube with a length of 16 nm long and 6.5 nm of radius.
- for the outer tube, a [18,12] nanotube with a length of 35 nm and 9.9 nm of radius.


Because the pair of integers [n,m] for the tubes are proportional, the two tubes have the same orientation.

The simulation of the system shows no difference of motion compared to the straight tube in the sense that the screwed orientation of the tube does not generate a rotating (screwing) motion of the tubes.

We will then try to initiate the rotating motion by constraining the outer tube to rotat.
 

 
The simulation was run at 300K with the same tubes as before.

We now see that the rotation of one tube generates a rotating motion in the other tube, it could be defined as a screwing motion. However the motion is not just the screwing motion of the tubes but also the sliding of one on the other (animation).

In fact the screwing motion of the inner tube generates a sliding in the screwing direction. The sliding then slows down because of the friction and the motion is again reinitialized by the rotating motion. Thus, the motion of the system is in fact a combination of a rotating motion and a sliding motion. The motion of this system can be compared to the motion of a tube on a graphite substrate which consists of a combination of rotating and sliding motion [9].
 

As expected the inner tube goes in the reverse direction when we reverse the rotation of the outer tube (animation).

We can see in these simulations that the motion of the tube is governed by the friction of the tubes. We will now try to measure the friction between the tubes.
 

In order to measure the friction coefficient, we will constrain one tube to move and the other to be fixed. It has been observed that the sliding motion is predominant compared to the rotating motion, there must be different friction coefficients corresponding to the two motions.

We will do these simulations with a straight nanotube system since we have seen that the screwed nanotube motion is made of a combination of rotating and sliding. Because we want to prevent any other motion from happening we will run the simulation at the lower temperature of 100K. Since we see that the evolution of the temperature does not "blow up" but consists of periodic oscillations when sliding and rotating the outer tube, we do not have to use a heat bath.

Taking the warm-up period of the temperature into account, we can estimate the sliding friction coefficient of 7.8E-13 +/- 2E-13 N/atom and a friction coefficient for rotating of 3.0E-12 +/- 1E-12 N/atom for straight nanotubes.

Although these friction coefficients have not been measured experimentally, the friction coefficient for sliding can be compared to the friction measured in another nanotube device such as the 8 walled nanotube and the friction of a nanotube on a substrate. The sliding friction coefficient measured differs by a n order of 1 to 10 compared to the experimental data collected. This difference can be due to the different systems studied and by the fact that these coefficient are not trivial to measure in experiments and in simulations.

However, the results seem consistent with our study of the motion since the friction coefficient for rotation is on the order of 10 more than the sliding friction. This explains why the sliding motion is preferred to the rotating motion.
 
 

---