Mean Field Theory

    The Coulomb interaction between charged colloidal particles dispersed in a polar solvent is moderated and mediated by a diffuse cloud of surrounding ions. These simple ions are much smaller than the macroionic colloid, and carry much smaller charges. The resulting disparity in dynamical time scales encourages us to define an effective colloidal interaction averaged over the simple ions' degrees of freedom. How to define and interpret this effective interaction has inspired spirited debate for more than 50 years.

    Experimental observations reported over the past few years have raised the surprising possibility that like-charged colloidal spheres sometimes attract each other. If we view the spheres in isolation, their attraction seems counterintuitive. Recalling instead that the overall suspension is electro-neutral suggests that unexpected features in the spheres' effective pair potential must reflect unanticipated dynamics in the simple ions' distributions. The phenomena discussed in the following sections are noteworthy because they appear to be inconsistent with existing mean field theories. Such discrepancies raise concern about mean field theory's broader application to macroionic problems as diverse as protein folding, DNA complexation, and the stability of industrial suspensions.

    Since the goal of this Article is to assess constraints on theory imposed by experimental measurements of colloidal interactions, it is worthwhile to review the theory's principal approximations.

    Virtually all descriptions of macroionic interactions take advantage of the separation of time scales between the macroions' and simple ions' motions and describe the simple ions as moving in the field imposed by stationary macroions. The partition function in this Born-Oppenheimer approximation is

$ Q = Q_0 \int_\Omega d\vec r_1 \cdots d\vec r_N \, \exp \left[ - \beta V\left( \left\{\vec r_i\right\} \right) \right],$
$ V\left(\left\{\vec r_i\right\}\right) = \frac{1}{\epsilon} \sum_{i=1}^N q_i \phi (\vec r_i)$

V(r) is the electrostatic potential energy for  N simple ions with charges qi arrayed at positions ri in an electric potential f(r). The prefactor Qo results from integrals over momenta and b-1=kBT is the thermal energy at temperature T. All charged species in the system, including the fixed macroions, contribute to f(r).  The macroions also exclude simple ions from their interiors, so their volumes are excluded from volume of integration W.

    The partition function can be rewritten as a functional integral over all of the possible simple-ionic distributions

$ Q = Q_0 \int^\prime Dn \, \exp \left( - \beta f [ n ] \right),$

$ n (\vec r) = \sum_{i=1}^N \delta (\vec r - \vec r_i),$

where n(r) is one particular distribution whose activity is approximately given by

$ f[n] \approx V[n] + k_B T \, \int_\Omega n \ln n \, d\Omega.$

Minimizing f[n] to implement the mean field approximation yields the familiar Poisson-Boltzmann equation

$ \nabla^2 \phi = - \frac{4\pi}{\epsilon} \, \sum_\alpha n_\alpha q_\alpha \exp \left( - \beta q_\alpha \phi \right),$

where the subscript a denotes the various species of simple ions. The fixed macroions provide boundary conditions for f(r). 

    By considering only one possible ionic distribution, the mean field approximation ignores contributions from fluctuations as well as higher-order correlations. Even this simplified formulation is intractable for all but the simplest geometries. In developing the classical theory for colloidal electrostatic interactions, Derjaguin, Landau, Verwey and Overbeek  (DLVO) invoked the Debye-Hückel approximation, linearizing the Poisson-Boltzmann equation, and solved for the potential outside a sphere of radius $ \sigma$carrying charge -Ze. The decay of correlations within the simple ion distributions is described by the Debye-Hückel screening length, $ \kappa ^{-1}$, given by

$ \kappa^2 = \frac{4 \pi}{\epsilon k_B T} \, \sum_\alpha n_\alpha {q_\alpha}^2.$

    The Debye-Hückel approximation cannot be valid near the surface of a highly charged sphere. The hope, however, is that nonlinear effects will be confined to a small region very near the sphere's surface and thus may serve only to renormalize the sphere's effective charge at longer length scales.

    We obtain the effective pair potential by integrating f[n] over the surface of a second sphere separated from the first by a center-to-center distance r. This integration is facilitated by assuming the second sphere's presence does not disrupt the first sphere's ion cloud. The resulting superposition approximation yields a screened Coulomb repulsion for the effective intersphere interaction,

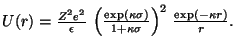
 $ U(r) = \frac{Z^2e^2}{\epsilon} \, \left( \frac{\exp ({\kappa \sigma})}{1 + \kappa \sigma} \right)^2 \, \frac{\exp ({-\kappa r})}{r}.$

    The DLVO theory was developed principally to explain colloidal suspensions' stability against flocculation under van der Waals attraction. In general, U(r) should include an additional term accounting for such dispersion interactions. However, their influence is negligible for the systems we will consider and is omitted.

Reference: http://griergroup.uchicago.edu/~grier/granada/node1.html