Summary of Computer Simulations
Charged Particles in a Uniform Electric Field
Introduction and Overview
This set of simulations adds a uniform electric field to the
charged gold particles and observes the results. Note that this experiment has
not been conducted before in a labratory, so there are no experimental results
to compare with in this case.
This set of simulations involved placing particles randomly on a 500 × 500
lattice, each with a charge of +1.6e-19 Coulombs, or -1.6e-19 Coulombs. The net
charge of the system is zero. That is, the number of particles placed was
always even, and half were always positively charged, while the other half were
always negatively charged.
An uniform electric field was also applied. Note that clusters formed from
equal parts positive and negative charge have no net charge, and are thus
unaffected by the electric field.
For the purposes of this simulation, a moderately strong electric field was
applied. While it would be interesting to explore how the strength of the
electric field affects the observed properties of the clusters, time
constraints did not allow us to explore that fully. However we have some
preliminary results for a strong electric field to show in the form of a movie.
Images
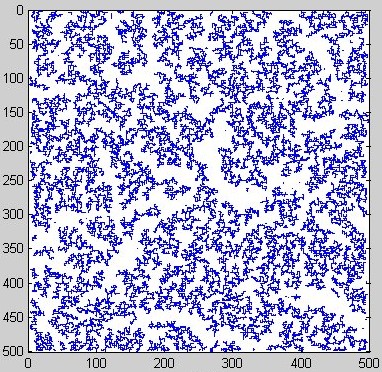
The following image shows a typical end configuration.
Simulations and Results
The following simulations were run to determine the relation between the average cluster size, the number of clusters, and the simulation time:
- A 500x500 system of 52,500 atoms (21% coverage).
- A 500x500 system of 47,500 atoms (19% coverage).
3. A 500x500 system of 27,500 atoms (11% coverage).
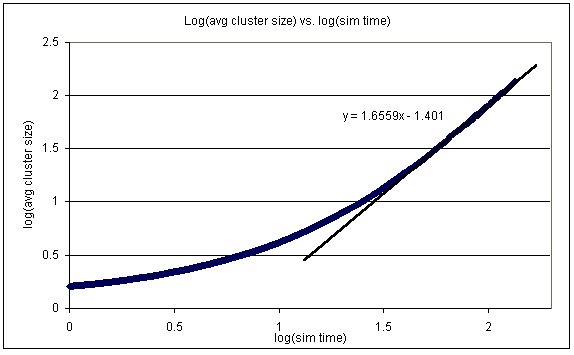
A sample plot of the average cluster size vs. the simulation time is shown below.
A sample plot of the number of clusters vs. the simulation time is shown below.
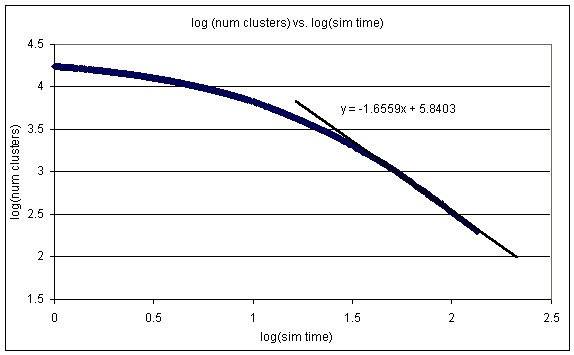
Note that for our simulation, as the number of particles is conserved, the average cluster size and the total number of clusters are not independent variables. As such, our slopes (tabulated below) will have the same error bars, and will differ only by a sign. In the experimental case, these two variables are not independent, so we have compared our (dependent) results to their (independent) results for the sake of completeness.
The following data was observed:
|
Coverage |
Slope of log(avg cluster size) vs. log(sim time) |
Experimental Results |
|
21% |
1.971 +/- 0.004 |
Unknown |
|
19% |
1.905+/- 0.003 |
|
|
11% |
1.656 +/- 0.002 |
|
Coverage |
Slope of log(#clusters) vs. log(sim time) |
Experimental Results |
|
21% |
-1.971 +/- 0.004 |
Unknown |
|
19% |
-1.905+/- 0.003 |
|
|
11% |
-1.656 +/- 0.002 |
The following simulations were run to estimate the average fractal dimension for various coverage densities:
- A 500x500 system of 10,000 atoms (4% coverage).
- A 500x500 system of 30,000 atoms (12% coverage).
- A 500x500 system of 52,500 atoms (21% coverage).
- A 500x500 system of 57,500 atoms (23% coverage).
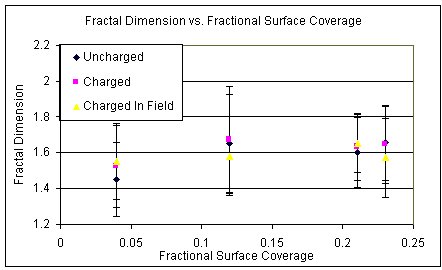
For simulation #4 :
Average fractal dimension computed to be 1.55 +/- 0.21
For simulation #5 :
Average fractal dimension computed to be1.58 +/- 0.22
For simulation #6 :
Average fractal dimension computed to be 1.65 +/- 0.16
For simulation #7 :
Average fractal dimension computed to be 1.57 +/- 0.22