We have written a series of computer programs in
both C and Mathematica to
simulate protein folding with a Simple Exact short chain model. Unlike most
other "toy models" of this nature, we include second nearest neighbor
interactions in one version of our code.
A protein is a long sequence of the 20 possible amino acids. This sequence
collapses to a "native structure", which determines its biological
activity. This structure is often very complex, and yet the protein
collapses from the denatured state to the same structure every time. The
problem is the following: how does a sequence of amino acids choose, and
then fold into, this one particular "native" structure out of the huge
phase space of such structures available to it? The protein takes anywhere
from a millisecond to a few seconds to fold: this is far less time than it
takes to search through the states available to it. [1]
A well designed protein must be able to avoid large sections of the conformation
space in order to fold in a timely fashion. A "good" protein is
one that has negligible degeneracy at low energies: thus it folds to the
thermodynamically lowest energy state without getting stuck in nearby
metastable states. Designing a protein, therefore, has two themes:
"positive design", which provides a low energy state, along with a pathway
to get there, and "negative design", i.e. there should be no other states with
similar energy that the protein might accidentally fold to.
Various approaches have been taken to solve the protein folding problem. A
top-down solution involves "Taxonomic" [1] methods, by which large
catalogs of known proteins are compared in all their complexity. (Some of
these databanks can be found in the links of interest
below). Computer
models are used in the opposite sense: from bottom up, using the modelled
underlying mechanisms to generate the protein structures. There are many
versions of these models, ranging from the general which only investigate a few
conformations of the large number available, to simple exact models, which
consider all possible conformations. Simple Exact models, while limited in scope
due to sheer computing power issues, enable the calculation of the
partition function and related quantities.
Our aim with this project was to research and develop a simple exact
model, which was extended to include second nearest neighbor interactions.
We simulated various sequences of amino acids and their resulting
conformations.
By analyzing the degeneracies of the energies, "good" protein sequences
can be seperated from the "bad" ones, using the ideas of degeneracy with
positive and negative design outlined above. In other words, our goal was
an amino acid sequence and a set of monomer interaction rules which would
show a small number of conformations with very low energy. It is believed
that seeing such behavior in simple exact models demonstrates the fundimental
aspect of protein behavior.
The standard exact model proposed by Dill [1],[2] is called the "HP
nearest neighbor model". In this model, there are only two types of amino
acids used: H for hydrophopic and P for polar. Proteins tend to arrange
themselves such that the H are folded in on, and the P are at the
interface with the water surrounding the molecule. The energy of the
conformation is calculated by the nearest-neighbor interactions (NOT
counting the interactions between bonded H and/or P, which are those
linked together on the sequence chain). Usually, all are neglected except
for H H which is -1. Such models are based on the experimental observation
that conformations of real proteins almost always bury hydrophobic
amino acids, keeping the polar monomers on the surface.
We wrote a computer program that calculates all possible conformations
from a set of complete permutations of the moves up,down,left,and right. A
possible conformation is one which does not try and put an amino acid on
an already occupied site. Of the sucessful conformations, the energies are
calculated for two situations: nearest neighbor only, and both nearest
neighbor and second nearest neighbor interactions. Additionally, we enable
up to four different amino acid types to be input in the sequence, and we
have a user input table of the interaction energies between all of them
to enable easy modification of the model.
Following are selected results from our simulations. First, a simple
example of a 6-chain is presented. The possible conformations and their
energies are placed in a histogram, which illustrates the degeneracies of
various energies.

Second, the difference between two different sequences, and the expanded
model with second nearest neighbor intereractions, is presented.
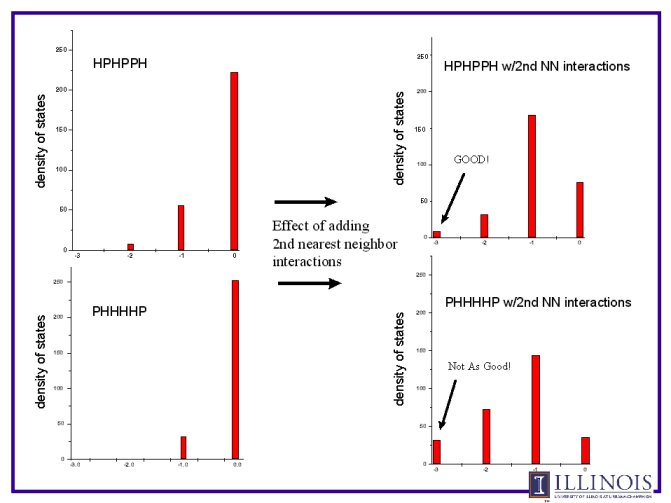
Note here that there are two different effects. One is the sequence of the
protein only. the HPHPPH is a "better" protein than the PHHHHP, becuase it
can both achieve a lower energy state, and has a lower degeneracy at that
state.
The second effect is that of the nearest neighbor interactions. The energy
graphs show more clearly the trends of degeneracy, and in both cases lower
energy states are reached. However, the lowest degeneracy of the first
sequence is again very clearly realized at all lower energy conformations.
We believe simple models such as this are fundamental to understanding
protein folding. The sequence itself is the key to why the protein folds
as it does, and sequential effect is very evident even in our very basic
model. Additionally, considering second nearest neighbors may be of use in
analyzing the density of states of the protein, and deciding what is a
"good" vs. a "bad" sequence to perform further studies on.
References:
[1] Chan, Hue Sun. Dill, Ken A. "The protein folding problem" Physics
Today v.46 (Feb. 93), p 24-32.
[2] Dill, Ken A. et al "Principles of protein folding- A
perspective from simple exact models"Protein Science (1995),
4:561-602
[3] Nunes, Nicole L, Chen, Kaiqi, Hutchinson, John S. "A flexible lattice
model to study protein folding" J. Phys. Chem (1996), 100:
10443-10449
Additionally, the Project Links below all
provided helpful information and should be considered as references.
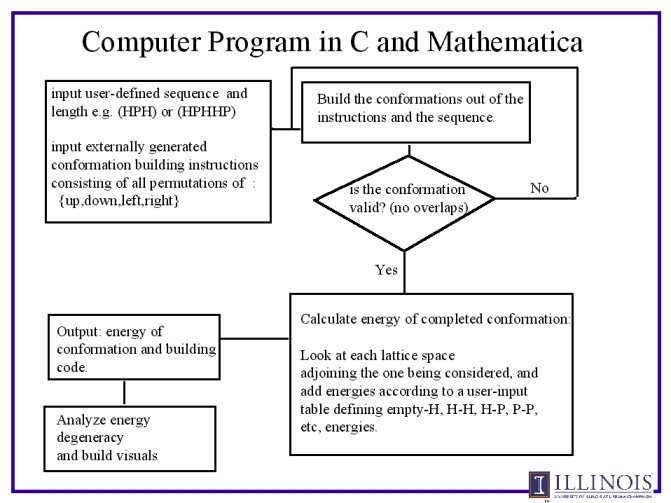
Our computer programs. Note flow chart is included after list.
Main C files (we compiled/ran on the sun engineering workstations)
Input Files:
"energies.dat": the input energy
table. This version has HH=-1 interactions only.
Mathmatica generation and viewing files
- drawPicture Mathematica program to
generate pictures of a protein given the conformation and monomer sequence.
Pictures are saved as gif files.
- inputFileMaker2 Mathematica program
to generate input files (like inputinst.dat) which enumerate all possible
conformations
Flow chart of the computer
programs
some useful web links:
This is the inital abstract presented to the class.
Protein Folding Simulation Project: Abstract 10-15-98
Tim Dellinger
Jennifer Gerbi
Ioannis Tziligakis
Protein folding studies investigate the mechanism by which a
protein molecule obtains an observed preferred spatial orientation, or
conformation. Proteins are complex molecules, and these studies have
involved correspondingly elaborate computer simulations. Nevertheless,
there are many unanswered questions in this field, and the topic is very
active.
We propose to investigate the computer simulation method of
protein folding by researching and developing a simple model of this
phenomenon. Small, two dimensional "pseudoproteins" will be used, with the
molecule consisting of only "a" and "b" amino acids (e.g. a-b-a-b-b-a-a-b
etc.) on the order of 16 units long. A lattice model will be used, by
which the units can only move to a chosen set of coordinates.
Additionally, only nearest neighbor interactions will be considered to
define the potential. The metropolis monte carlo technique will be used
to "anneal" the molecule. Depending on the temperature, the amino acid
sequence in the chain, and the initial conformation of the chain, a number
of different transitional and final conformations are possible. Our goal
is to develop an energy minimizing algorithm to find the energetically
preferred conformation, and to maximize the efficiency of this
algorithm.
Using our program, we will contrast the characteristics of various
systems by varying four items: the anneal temperature, inital protein
conformation, initial protein sequence, and nearest neighbor potential.
We will investigate and compare certain properties of each system,
including the relaxation time that it takes for the molecule to reach the
final preferred conformation, the metastable conformations and energies,
and the final conformation and energy.
Finally, it would be of interest to investigate some of the three
dimensional, more complex models that are available for immediate use.
Running simulations under similar beginning conditions to our model would
enable us to very roughly contrast our results, and gain insight on what
has been accomplished in the field recently.
gerbi@uiuc.edu