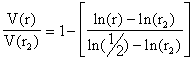
An active walker algorithm consists of several essential components. There must be a selection algorithm for choosing which walker will walk. In our codes, this selection is made with equal probability for each available walker. There are further selections of which space to walk into and whether that move occurs or not. In our code, an adjacent space is picked at random. The space is immediately rejected if occupied. If unoccupied, the space is filled with a probability proportional to the value of the landscape function. Lam and Pochy implement a similar algorithm [Lam, 1993 #4], however, our algorithm uses the sum of the surrounding landscape in choosing whether a walker will walk before choosing a direction.
The next important component is a landscaping function to modify the potential. In this case the landscaping function approximates diffusion of the solute or thermal energy. It is unreasonable to solve the diffusion equation for the entire matrix not only due to the long computation times involved but also because the growth occurs in discrete packets which would result in an aphysical flow of solute or energy. Instead, the diffusion equation is approximated only locally for each growing element. The method finally used was to approximate the steady state, radially symmetric diffusion profile for a perfect sink as the landscaping function. In this case the value of the landscape function, V, is rescaled using the following formula,
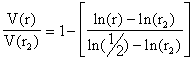
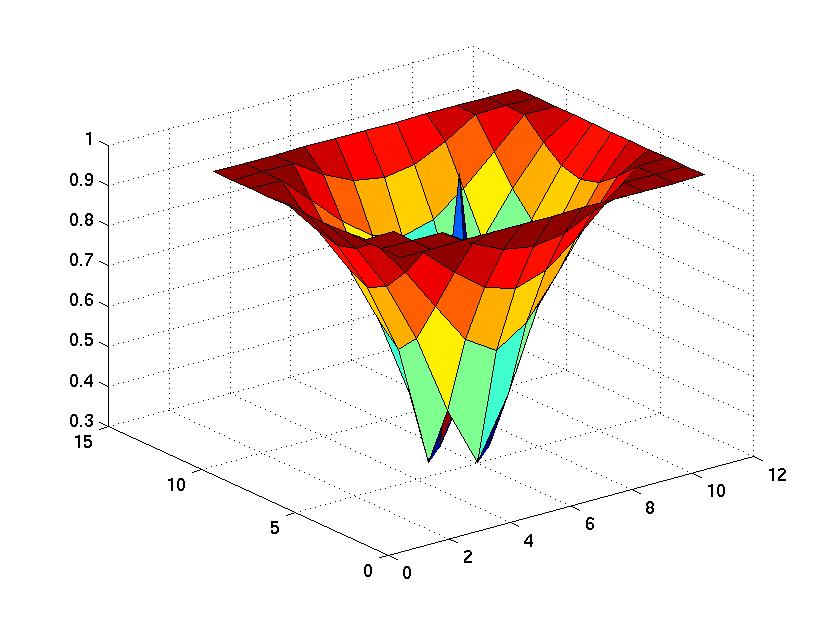
where r is the radial distance from the newly filled space, and r2 is the maximum radial distance at which the landscape function is affected, or interaction range. The interaction range is a function of the ratio of volumetric concentration in solid to that in the liquid as well as the diffusion coefficient for the process involved. A surface plot of the landscaping function for an interaction range of 5 is shown below.
To reduce the number of walkers that must be accounted for in large structures, a walker is removed from the active list when the sum of the surrounding landscape results in a total probability of walking of less than 0.001.
The random walker code is simply implemented by placing a particle on a toroidal grid and allowing it to walk until there is a collision with a stationary particle. When there is a collision, the particle may become stationary with some sticking probability or it may continue to walk. In both active and random walker cases, a single seed particle is used to start growth.
Source codes for both active and random walkers are available here.