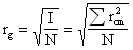
The radius of gyration is another useful value for describing fractal patterns. The radius of gyration, rg, is defined as the radius at which a point of mass (or number of filled spaces, N, in this case) equal to that of the entire pattern would have to be placed to have the same moment of inertia, I. The moment of inertia itself can be calculated in terms of the number of particles from the sum of the square of the distance of each particle from the centroid, rcm, so that the radius of gyration is given by the following equation.
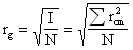
The following graphs show the trends of radius of gyration for active and random walkers respectively.


Both graphs show the values obtained for 1000 particles using a linear fit over the nearest 100 points to lessen variations.
The active walker shows a more dramatic increase than the random walker. This follows directly from the trends in fractal dimension which indicate a more fibrous limit for active walkers. For a similar number of particles, the more fibrous pattern must have a large portion of its area farther from the centroid.