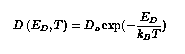
The Theory Behind

In this work we implemented two different Kinetic Monte Carlo algorithms. Both of them are working on the same principles, however, the second one utilizes a better scheme for advancement of time and is much more efficient. We will summarize both of them here. The algorithms will be called KMC1 and KMC2, respectively.

As compared to Metropolis Monte Carlo Methods, KMC has a different scheme for the generation of the next state. The main idea behind Kinetic Monte Carlo is to use transition rates based on a dynamic model, with time increments formulated so that they relate to the microscopic kinetics of the system. It is also important that during simulation effective independence of events be achieved, by using small enough time steps.[1,2]

Metropolis like methods utilize the energy difference between states, to decide on a move, whereas KMC methods utilize rates that depend on the energy barrier between states. For the simulation of MBE growth of monatomic crystals the diffusion on the surface is determined by the energy barriers that exist for the breaking the substrate and the neighbor atom bonds.[3,4] Also, for atoms, that will be taking a step down the edge there is an additional barrier, which is called the Ehrlich-Schwoebel barrier.

Then the rate for surface migration by hopping to a nearest neighbor site is determined by the following formula:

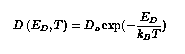
The characteristic frequency, also, is a function of the temperature.

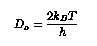
The total barrier, without taking the Ehrlich-Schwoebel barrier into consideration is taken as:

Ehrlich-Schwoebel barrier, Es, is also added to this value, when necessary.

Within this theoretical model of the surface movements, the KMC1, algorithm uses a fixed time step, that is chosen such that:

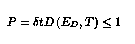
The probability needs to be smaller than one if you sample the atoms uniformly, so that the different events in consecutive time steps would not be correlated.

The KMC1 algorithm proceeds by testing each atom for hopping by comparing the above probability by a random number. The problem with this approach is that , except for the very small simulations, there are usually lots of atoms with very small probability of hopping. Still, KMC1 tests all of them for movement. The end result is that lots of CPU time is lost by doing nothing.

KMC2 algorithm proceeds by ordering the atoms into lists according to their probability of migration. The total probability of the movements is normalized to one. A random number is used to determined to which atom will move, by weighting the random number by the total probability of movement in a group.[5,6] So the move is always accepted for each time step.The time step is determined by the average hopping rate of all the atoms and will change as the configuration changes. The advantage of this algorithm is you basically avoid testing and rejecting all the less-movable ones since their weighting ration is very small in the probability list. You are safe to doing so if the time steps are much smaller than other time scales in the simulation.A