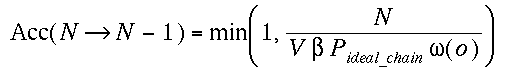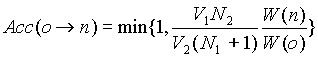Algorithms
Take a look at what's going on during the simulations
before we discuss the algorithms.(No volume change and chain exchange.
Suggested browser:IE5.0)

In this project, we use grand canonical ensemble to calculate
the absorption curve of polymers from resevoir, and we use Gibbs ensemble
to calculate the phase diagram of gas-liquid polymers. The difference of
the two ensembles is that, in the former one, we are concerned with one
system and treat the other as a resevoir and its effect comes in through
pressure as well as particle exchange. We need only to keep track of physical
quantities in the first system. And that, in the latter one, we are
concerned with both of the systems and they equilibriate through volume
change and polymer exchange. We have to record physical quantities in both
systems. In the following, we do not give the derivations of the acceptance
ratios. We simply describe the procedures and refer those interested to
the literature3.
Algorithm in Grand Canonical Ensemble
There are four different kinds of Monte
Carlo procedures in the grand canonical ensemble:(i)Displacement of chains,(ii)Deformation
of chains,(iii)Change of volume and (iv)Insertion/Removal of chains.
(i)Displacement of chains
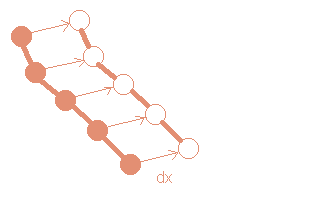
A chain is randomly selected and moved to a new position.
This trial move is accepted with a probability

(ii)Deformation of chains
In addition to the configurational-bias method, we also
compare with the reptation method, so we list both algorithms as follows,
(a)Reptation
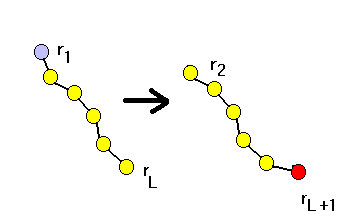
This involes selecting a chain, cutting one end and attach
a new monomer to the other end. Since the potential energy is composed
of two parts:bonded and nonbonded,
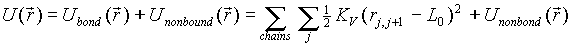
we can in practice sample the position(rL+1)of
the new monomer to be attached to one end, say rL ,according
to the bonded part,

Then we attach this new monomer and delete the other
end, say at r1, with an acceptance probability

Note that we have equal probability to choose either
end to be deleted.
(b)CBMC method
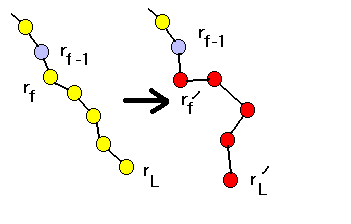
The configurational-bias method involve randomly selecting
one monomer in a chain and replace the rest of the chain with a new configuration,
which is generated in a biased way such that this new configuration is
most probably accepted. We must determine the Rosenbluth weight W(o) of
the old configuration from rf to rL and W(n)
of the new configuration from rf' to r'L . The new
configuration is accepted with probability

Next we discuss how to determine W(o) and W(n).
For W(o):
(1) Measure the interaction energy of the f-th monomer
with other polymers as well as with monomers before the f-th one and denote
the value by uf(o) and define wf(o)=k exp(-buf(o)),
where k is the number of random directions we assign to our continuum model.(Note
k=6 is the coordination number in 3-d cubic lattice.)
(2) Compute for the i-th monomer the nonbonded interaction
energy(ui(o)) with other polymers and previous monomers. Generate
k-1 directions randomly and a bond length l according to the bonded distribution,
and we get k-1 new positions.
Suppose our i-th monomer were in one of the k-1 sites,
say j, and calculate its nonbonded interaction with other polymers and
previous monomers, denoting the value by ui(j). And define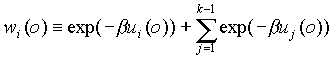 .
.
(3) Repeat (2) until the end of chain. The Rosenbluth
weight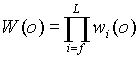 .
.
For W(n):
(1) Generate k directions randomly and a bond length
l according to the bonded distribution, and we get k new positions. Measure
the interaction energy uf(j) and calculate  .
For the k possible new positions, choose one, say n, with a probability
.
For the k possible new positions, choose one, say n, with a probability  .
.
Note, if f happens to be one, this means that we grow
a whole new chain. And we generate the first monomer at a random position.
Its interaction energy with other polymers is denoted by u1(n)
and the w1(n) is defined as 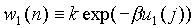 .
.
(2) Similarly, calculate wi(n) and choose
one with a probability 
(3) Repeat (2) until the end of chain. The total nonbonded
interaction energy of the new grown part is 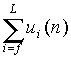 and the Rosenbluth weight
and the Rosenbluth weight 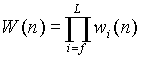 .
.
(iii)Change of volume
When make a volume change from V to Vnew,
we
accept the trial move by an acceptance ratio,
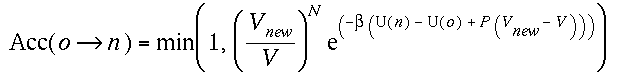
If instead we perform the random walk of volume change
in ln V, the probability of accepting this ln Vnewis
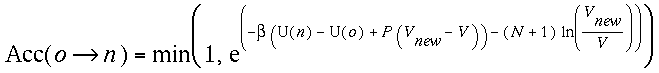
(iv)Insertion/Removal of chains
(a)Insertion
We grow a whole new chain (see note in CBMC method)
and compute W(n). We define the normalized Rosenbluth weight 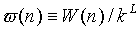 , where L is the number of monomers in a chain. And accept this new chain
with a probability,
, where L is the number of monomers in a chain. And accept this new chain
with a probability,
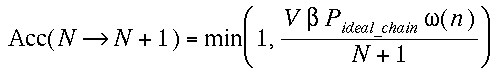
where Pideal_chain is the pressure of the
resevoir of ideal chains.
(b)Removal
We randomly choose an existing chain, compute its W(o)
and define the normalized Rosenbluth weight 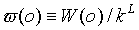 .This chain is deleted with a probability,
.This chain is deleted with a probability,
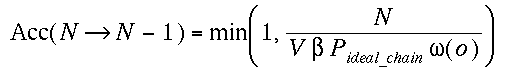

We use the grand canonical ensemble to simulate the adsorptiion
curve of polymers from a resevoir of ideal chains. We use 40 displacements,
20 CBMC moves and 20 Chain exchange in a cycle and average over 2000 samples
after 2000 equilibriiation steps.(Click on the graph to have an enlarged view.)
Algorithm in Gibbs Ensemble
The two procedures, displacement and deformation of chains,
are the same as those in grand canonical ensemble, and they are performed
independently in each box. But increase of the volume of one box decreases
that of the other, and the insertion of a chain into one box means removal
of a chain from the other box at the same time.(We keep total volume and
number of chains constant.) So there needs some modification of the above
third and fourth procedures.
(iii)' Change of volume
Since total volume of the two systems is V=V1+V2=fixed,
if the volume of box 1 is changed to V1new=V1+dV
, box2 is then changed to V2new=V2 -dV.
The acceptance ratio for such change is,

If instead we perform the random walk of volume in ln(V1/(V-V1)),
we
accept the ln((V1/(V-V1))new)
with a probability,

(iv)' Exchange of chains
If we remove a chain from box 1 and insert it into box
2, we have to calculate the Rosebluth weights W(o) of box 1 and W(n) of
box 2. This trial exchange is accepted with a probability,
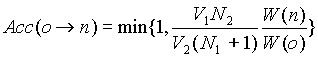
Note that we have equal probability of choosing to insert
a chain into or remove a chain out of a box.

We use Gibbs ensemble to compute the vapor-liquid coexistence
curve of the Lennard-Jones chains(6000 samples after 6000 equilibriation
cycles with initial 50 polymers in each system of box length 8.6). We estimate
the critical temperature Tc to be around 1.9+/-0.1 and
the critical polymer density to be 0.08+/-0.002.(Click on the graph to have an enlarged view.)
Back to
Project Main Page






![]()
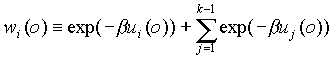 .
.
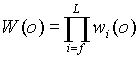 .
.
 .
For the k possible new positions, choose one, say n, with a probability
.
For the k possible new positions, choose one, say n, with a probability ![]() .
.
![]() .
.
![]()
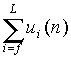 and the Rosenbluth weight
and the Rosenbluth weight 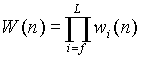 .
.
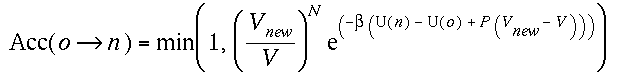
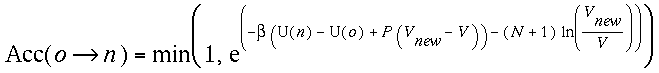
![]() , where L is the number of monomers in a chain. And accept this new chain
with a probability,
, where L is the number of monomers in a chain. And accept this new chain
with a probability,
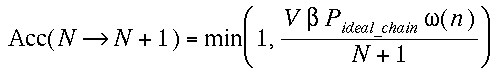
![]() .This chain is deleted with a probability,
.This chain is deleted with a probability,