To determine the desired points of phase transition we performed the
computations for each lattice at 23, 29, 35, 41, 47, 50, 53, 56,
61 and 65 K. The potential energies for FCC were computed at the equilibrium
lattice spacing of 5.649 A, and also at smaller lattice spacings to simulate
the increase of pressure to find its phase transition with the tetragonal
phase. The potential energies of the HCP lattice were computed at the equilibrium
lattice spacing of 4.039 A, c/a ratio of 1.651. We also computed the energies
at a spacing of 3.627 A to simulate its phase transition with the tetragonal
phase. This lattice spacing was determined through linear extrapolation
of the isothermal compressibility, and was, unfortunatley, much too small,
producing a pressure far higher than we had anticipated. The tetragonal
phase was computed with a lattice spacing of
5.596 A, with c/a ratio 0.9044, which corresponds to the physical lattice
at aprroximately 4 GPa. The energies determined within 20% of those measured
in experiment and from other calculations.
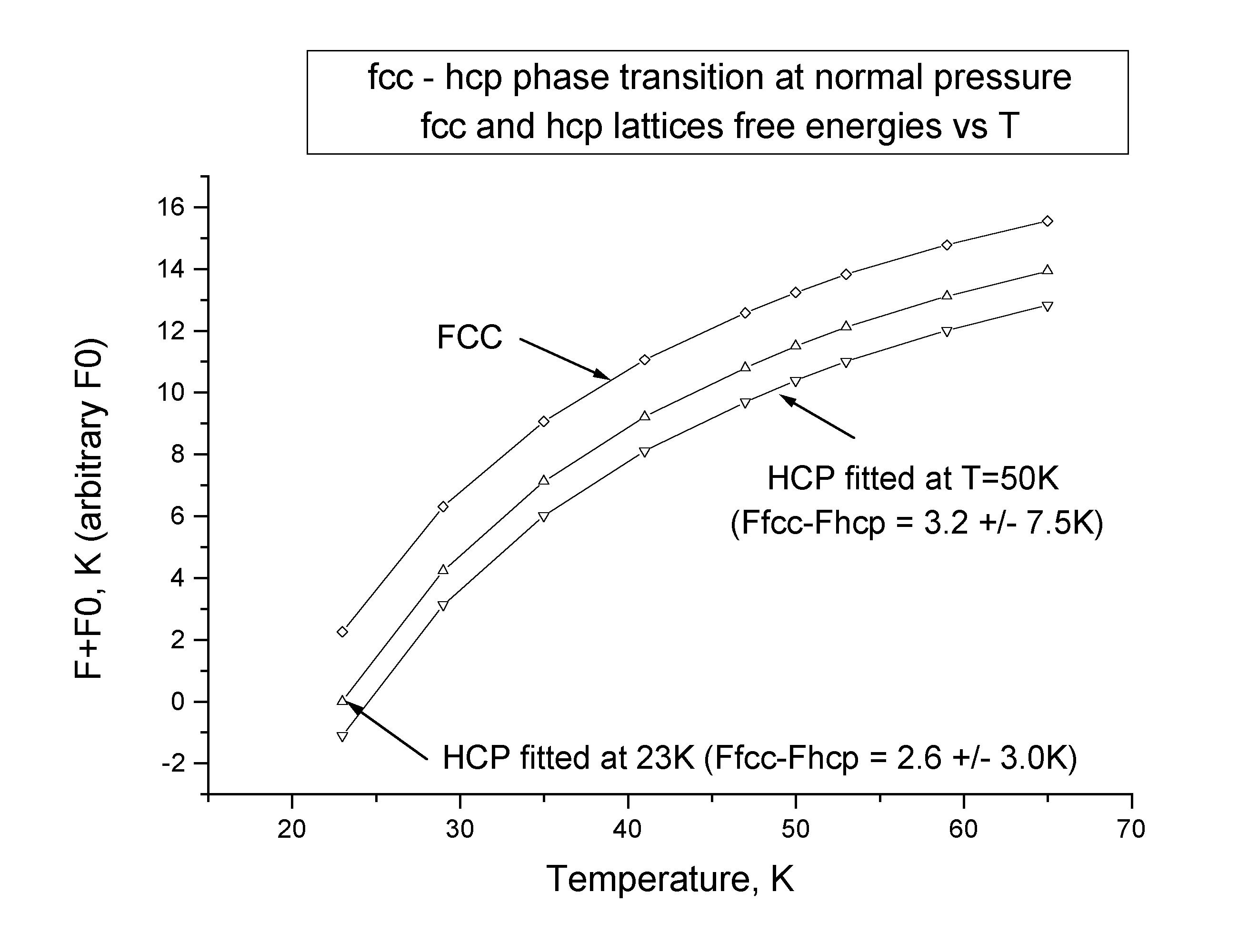
Our best result came from the FCC/HCP data. The graph below shows the
results of the free energy calculations of the FCC and HCP lattices. The
top curve is that of the FCC, while the bottom two are of the same HCP
data, fit to the two free energy differences we found. The error on the
free energies of specific data points has been left off the graph because
these errors are on the order of .1 K, while the error in the free energy
differences is larger than the calculated differences. The shape of the
free energy curves roughly follow those of other results, although we would
like to see the FCC free energy fall of faster than the HCP at low energies.
The temperature of the phase transition has been found experimentally to
be around 34 degrees.
 |
Using our extrapolated HCP lattice constant the HCP lattice energy was
far too high to hope to see the phase transition with tetragonal. We assume
this means that the pressure resulting from the change in lattice parameter
was too high.
Next: Conclusion/Further Study
Up to Table of Contents