Calculating the difference in free energies between two systems:

We have used Kirkwood's coupling parameter method[4]. In this method the potential energy of the system under consideration is gradually switched to the potential energy of the reference system according to the following formulae

such that

where denotes an ensemble average for a system with a potential energy function U(lambda). Lambda in this formulae runs from 0 to 1 corresponding to the potentials of the system under study and the reference system respectively.

We can then integrate this to find the free energy difference between the two systems,

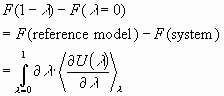As the reference system we used the system of rotors, each of which doesn't interact with the others. The condition of independence of rotational movements of the molecules in the lattice implies that the total partition function of this system can be written as:

Ztot = (Z1(T))^N, where N is the number of atoms, and Z1 is the partition function of a single rotator and depends exclusively on temperature.

It should be noted that since we are modeling perfect lattices with no translational and vibrational degrees of freedom Ztot has the same value (at the same T) for any type of lattice under consideration (in particular fcc, tetr or hex) as long as the number of atoms is the same.

The free energy of our systems at temperatures other than the reference temperature were found through integration over 1/T according to the formula

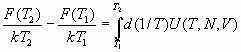at constant N,V.

The reference potential we used was

,

A similar calculation was made between the HCP and body-centered tetragonal phases at 50 K.

Unfortunately, the error in these calculations is a little large to get the desired results, as we discuss below.

Jordan et al. [3] mentions that "excluding long wave length compression modes, there are 21 translational and librational modes of which 17 are collective; the other 4 correspond to stretching of N2".

By fixing nitrogen molecules at fixed positions and thus completely excluding vibrational modes we could distort the patterns of weak interactions between these different modes. Given the smallness of the free energies of the phases that we studied (fcc) and (hcp) it might be that the omission of the weak interaction between vibrational and librational modes prevented us from observing the phase transition.
 

Up to Table of Contents
Next: The Code