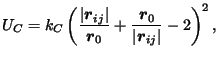Model

We investigate a two-dimensional network of a uniaxial nematic elastomer with variable asphericity subjected to a homogeneous deformation. The network consists of polymer chains with pendant nematic mesogens cross-linked with similar chains. Consistent with the coarse-graining approach mentioned earlier, each polymer chain can be considered as inhabiting an ellipse with a given asphericity $s=q+1$ ($s\geq 1$, with $s=1$ being a circle) and orientation $\boldsymbol{n}$. When the material is deformed, the network deforms, and both the asphericity and orientation of each ellipse change. To quantify the asphericity, we consider the area-conserving deformation of a circle of unit radius to an ellipse with semi-major axis $a$; then, the ratio of semi-major to semi-minor axis determines the asphericity. As before, the agglomeration, $\boldsymbol{A}$, is an order tensor which serves as the macroscopic measure of the nematically-induced distortion of the elliptical molecules comprising the network (Fried and Todres 2001). The network is modelled as points connected to springs. Each point has three springs connected to it so that it is trifunctional in nature. The points represent the network cross-links while the springs represent the polymer strands. This is in line with the view from the classical theory of rubber networks that the main contribution to elastic properties of the network derives from the polymer stands, which are, in essence, entropic springs (Everaers and Kremer 1996). An ellipse (or circle in the isotropic case) with one of its axes aligned along the spring can be thought to surround each spring, so that the asphericity can be determined depending on the deviation of the spring's length from its equilibrium value. In addition, the orientation of each ellipse is then the direction of its major axis, which is either coincident or perpendicular to the spring.

We account for various contributions to the overall potential of the system. The presence of pairwise springs between adjacent cross-link points accounts for the transfer of translational energy,

$$U_T = k_T ({\boldsymbol{r}}_{ij} - {\boldsymbol{r}}_0)^2$$

and the coupling between ellipse asphericity and spring extension or contraction,  

$$U_C = k_C \left(\frac{\vert{\boldsymbol{r}}_{ij}\vert}{{\boldsymb... ..._0} + \frac{{\boldsymbol{r}}_0}{\vert{\boldsymbol{r}}_{ij}\vert} - 2\right)^2,$$

where ${\boldsymbol{r}}_{ij}={\boldsymbol{r}}_j-{\boldsymbol{r}}_i$. Note that both $U_T$ and $U_C$ are minimized when the spring has its equilibrium length of ${\boldsymbol{r}}_0$. In addition, $U_C$ penalizes states in which the ellipses become too rod-like. Likewise, rotational energy can be transferred throughout the system by accounting for the relative angular orientation of the springs,

$$U_{\theta} = k_{\theta} (\theta_{ijk} - \theta_0)^2,$$

where

$$\cos(\theta) =\frac{{\boldsymbol{r}}_{ji}\cdot{\boldsymbol{r}}_{jk}}{\vert{\boldsymbol{r}}_{ji}\vert\vert{\boldsymbol{r}}_{jk}\vert}.$$

This angular term helps prevent the network from collapsing in on itself and the ellipses from overlapping on one another.