Results

In accordance with the simulation procedure described above, a series of experiments was run using 20 by 34 array of hexagons containing a total of 2760 cross-links (the particles) and 4027 agglomerations (the springs/ellipses). Extensional deformations imposed from zero through ten non-dimensional units were applied in unit increments to both top and bottom domain boundaries which were then held in place at their new positions. The following graphs show the initial configuration for the largest (20 unit) extension and its equilibrated configuration.

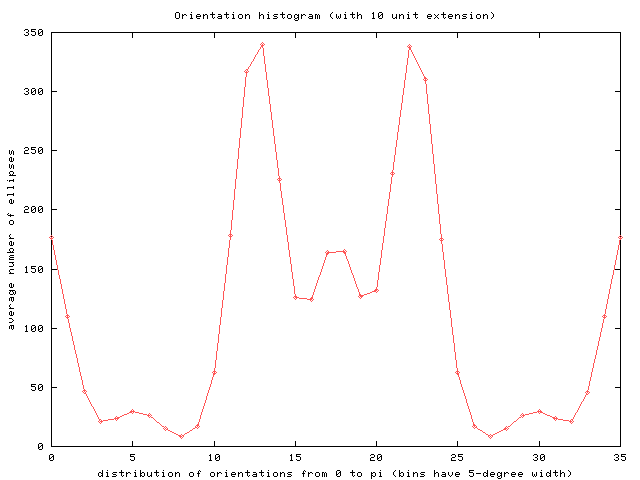
Monte Carlo runs were undertaken for each extension, and orientation distributions, average asphericities, and average widths were computed.

The histogram plots of orientation were binned only over equilibrated sweeps. For increasing extension, these plots show a greater tendency for the agglomeration to align with the direction of stretch $(\theta=\frac{\pi}{2})$. Note that the six peaks present in each graph correspond to the three unique directions occuring as the sides of the hexagons and their perpendiculars.

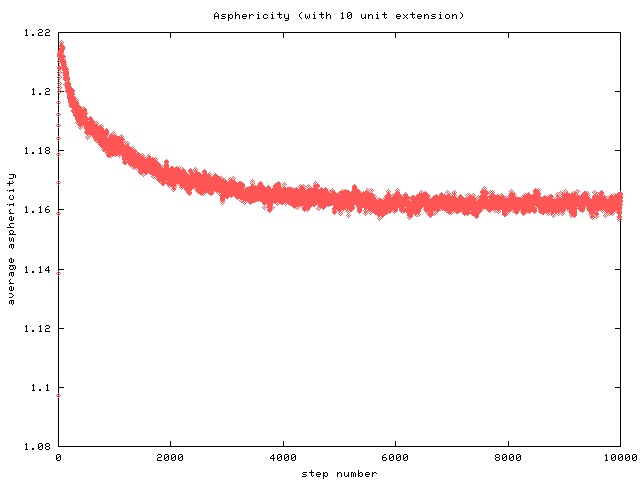
For non-trivial extensions, the plots of average asphericity show an early peak before settling down. This is because the springs attached to the cross-links on the upper and lower boundaries are initially severely strained as a result of the imposed deformation there. At this point, the rest of the network hasn't yet responded to relieve the stretch in those springs. So, correpsonding to this delay is a peak in the asphericity-entirely due to the stretched, boundary springs.

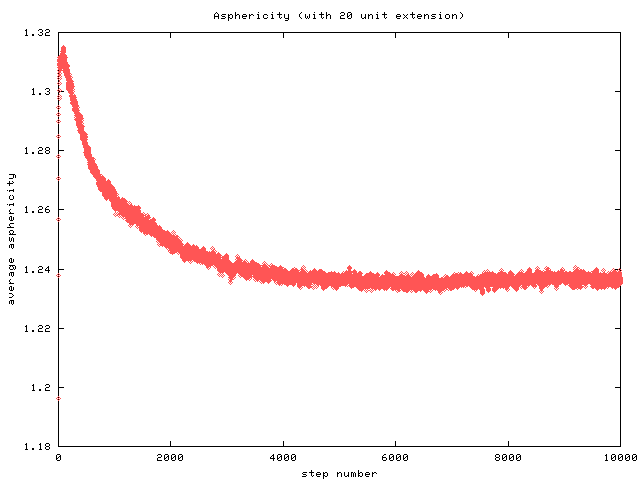
After some simulation time has elapsed, the rest of the network reconfigures itself to relieve the initial spike in the asphericity. However, for greater extensions, at equilibrium, the asphericity is seen to increase above the isotropic value of $1$. This trend makes sense since the imposed deformations cause the entropic springs to stretch and make it impossible for the agglomeration to remain circular.

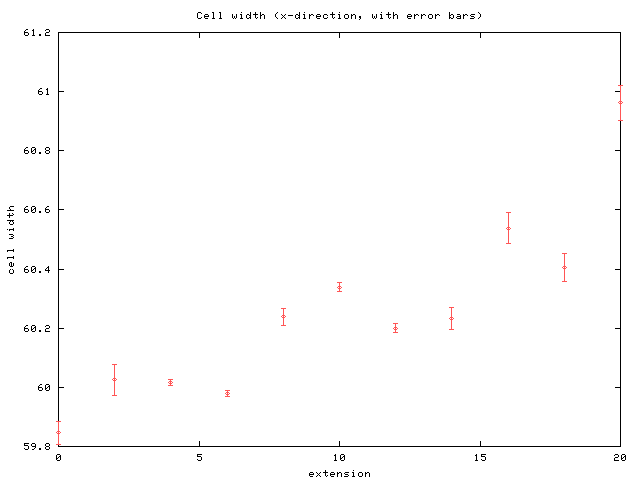
While the distribution of orientation and average asphericity show expected trends,

the results of computed average widths for various extensions are less encouraging. For our greatest, imposed elongation, there is actually a slight expansion in the lateral direction, contrary to physical reality for rubber networks.

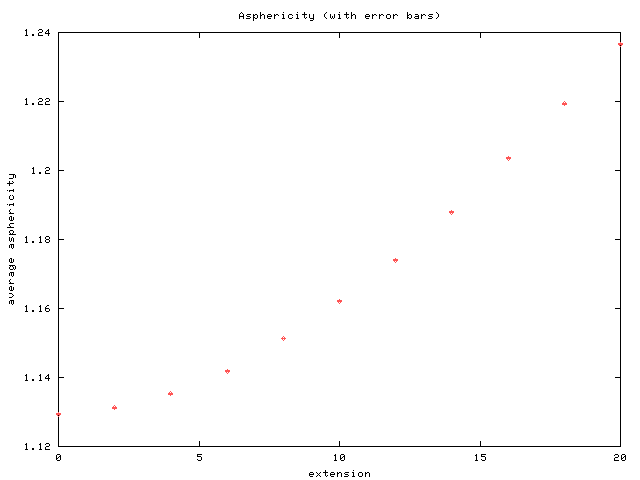
The following table lists the error in the mean for the average asphericity computed for $0,2,\dots,20$ unit extensions. Notice that the variance is so small that the error bars are not resolved on the accompanying plot.

mean	variance	correlation time	# effective points	error in mean
1.12934	$2.45386 \times 10^{-6}$	10.9708	182.302	0.000116019
1.13119	$2.35831 \times 10^{-6}$	9.95896	200.824	0.000108366
1.13529	$2.1547 \times 10^{-6}$	8.86313	225.654	9.77175e-05
1.14186	$2.07205 \times 10^{-6}$	9.90055	202.009	0.000101278
1.1513	$2.48441 \times 10^{-6}$	12.7529	156.827	0.000125864
1.16207	$2.11375 \times 10^{-6}$	11.2436	177.879	0.00010901
1.17405	$2.10461 \times 10^{-6}$	16.2805	122.847	0.000130889
1.18792	$1.89433 \times 10^{-6}$	14.8714	134.486	0.000118683
1.20353	$1.6501 \times 10^{-6}$	10.6	188.679	9.35175e-05
1.21929	$1.60384 \times 10^{-6}$	10.5706	189.204	9.20694e-05
1.2366	$1.30817 \times 10^{-6}$	8.55696	233.728	7.4813e-05

The source code used for the simulations is available.