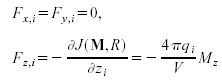Calculations
of Long Range interactions in 3D Systems with Reduced Periodicity
Anjan
Raghunathan
Sony
Joseph
Dept.
of Mechanical Engineering and Beckman Institute
Ewald Sums in 2D Periodic
geometries
Introduction
The evaluation of Coulombic interactions in large N-body systems is a common computational problem which is important with recent advances in simulations of biomolecular systems and nanotechnology. The most popular techniques are the Ewald, Particle Mesh techniques and the Fast Multipole methods (Pollock and Glosli 1996). In this project we review popular approaches for calculating long range interactions in 3D systems which are periodic in 2D (slab geometry) or 1D (wire geometry). Simulations were performed compare the accuracy of super cell approximation and corrected 3D Ewald for 2D periodic geometries.
Ewald Summation in 3D Periodic systems
The contributions to electrostatic potential at a particle i at ri due to other charges around it is expressed as:
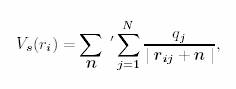
where
![]()
and
![]()
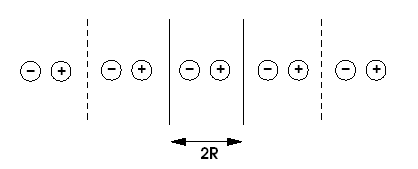
Figure 1: A 1D periodic system with box length =2R and
distance between charges =R
j=i term is omitted for the primary cell n=0. This sum is not absolutely but only conditionally convergent and has NboxxN2 operations. Ewald came up with an idea of splitting potential as a sum of two rapidly converging series: one in the real space and the other in the reciprocal k space.
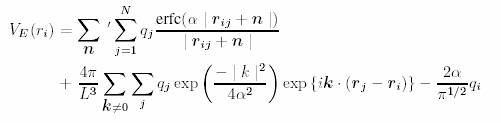
The term α is an arbitrary, but important parameter, which governs the relative convergence rates of the two main series. The last term is a `self-potential' which cancels an equivalent contribution in the k-space sum. We can make physical sense of it by noting that
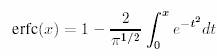
Thus the new series is a lattice sum of discrete charges and a point distribution as shown below in Figure 2. The choice of the smearing function influences the convergence of the series. Ewald used the Gaussian distribution for the spreading function which is normalized such that its integral from 0 to infinity is 1.
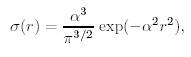
The parameter α decides the width and height of the spreading function and thereby the effective size of charges.
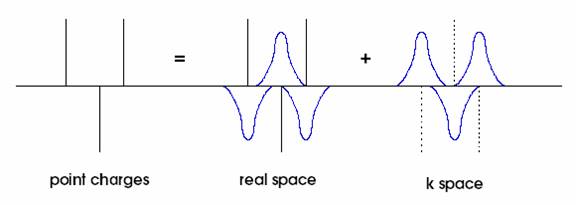
Figure 2: Splitting of charges into discrete and smeared
distributions in the real and reciprocal space.
The details of derivation can be found in Frenkel & Smith 2002 or Gibbon & Sutmann 2002.
![]()
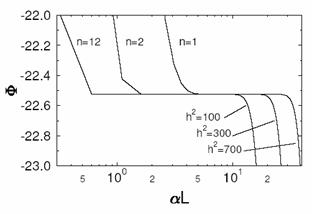
Figure 3: Potential versus αL
Optimal choice of the parameter αL is between 2 and 5. The parameter nmax and kmax can be chosen to get O(N3/2) operations using the relation below (Gibbon and Sutmann 2002)
![]()
where K is the reciprocal cut off distance, R is the real space cut off distance, exp(p) is the accuracy. Given R and p, K and α can be calculated. For small N<104 Ewald summation is suitable, but for larger systems Particle Mesh methods are preferred.
Particle Mesh Methods
The interparticle force is split into short range and long range parts in the PPPM method. The short range is calculated from particle-particle interactions and the long range is calculated from particle mesh methods. The long range interactions are calculated in the Fourier space using a grid. The charge is assigned onto the grid points using weighting function because originally charges are not located on lattice points. The poisson equation is solved for the potential using FFT or a diffusion algorithm. The forces are calculated by the derivative of the potential and assigned back to the system. The cutoff radius for long range and short range calculation are chosen to optimize accuracy as well as computational costs.
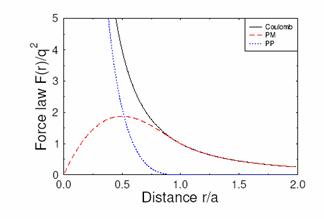
Figure 4: Left: The shaded area is the short range and gridded area is the long range part for a constant weighting function. Figure on the right shows split of PP and PM
The weighting function for assigning charges to the grid can be chosen in many ways. Figure 5 shows some of them. It should be an even function and the function should be normalized in such a way that sum of fractional charges equal the total charge of the system. Since the computational cost is proportional to the number of particles and the number of mesh points to which the single charge is distributed, a function with a small support decreases the computational cost.
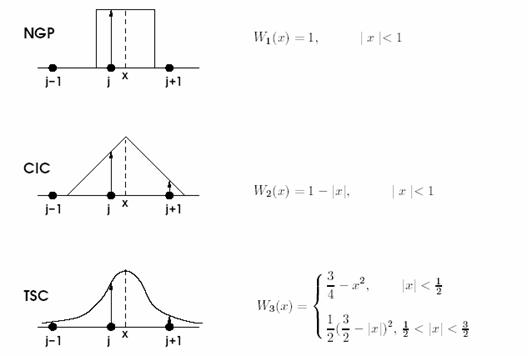
Figure 5 : Various weighting functions for charge assignment to a grid in PPPM.
Particle Mesh Ewald (PME) is a special case of PPPM where the parameter α is large so that the k space contribution becomes important. The charges are mapped into a grid and FFT is used to solve the poisson eqn. Since the grid size for FFT is mxmxm is proportional to N, the method is O(NlogN). The approach is as follows:
First the First we calculate the Fourier coefficient of the gridded charge density
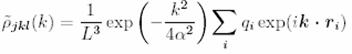
Potential in k space is
![]()
where
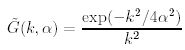
is the influence function and field is:
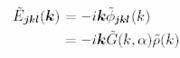
Inverse FFT yields potential and field which is used to update the simulation variables. There are many variations of PME. Smooth Particle Mesh method (SPME ) uses Euler splines to interpolate complex exponentials.
Ewald Summation in Reduced Periodicity
For many applications one is interested in a system that is finite in one dimension and infinite in the other two dimensions. Examples include fluids adsorbed in slit like pores, liquid gas interfaces or monolayers of surfactants. There could be also systems that are finite in two dimensions and infinite in the third dimension like flow in a cylindrical nanochannel or systems with wire geometries.
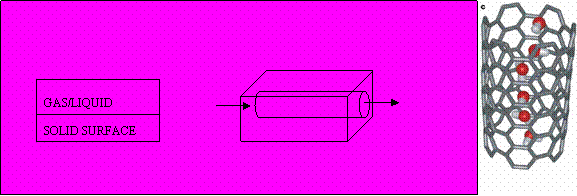
Figure 7: Various Applications that are 3D systems but are 2D or 1D periodic
In such inhomogeneous systems, special techniques are required to compute long range interactions. The obvious approach would be to use the same technique as the 3D Ewald summation, but restrict the reciprocal sum to vectors in the periodic direction only (EW2D).
The energy to be calculated is
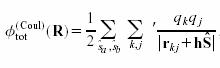
where periodicity is imposed only in 2 directions.
Methods based on Heyes et. al. (HBC)
Heyes, Barber and Clarke (1977) use a Fourier integral representation of the sum of Dirac delta functions that stand for the point charges of the system. They use the Gaussian integral to rewrite the inverse particle distance as
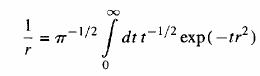
The integral is separated at 1/α2 and gives a short range part for the integral from 1/α2 to ∞, which corresponds to the complementary error function, and a long-range part for the integral from 0 to 1/α2 as in the classical Ewald method to give
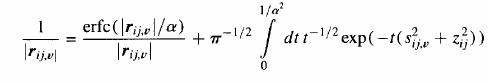
α is the screening parameter for the Gaussian charge cloud and is chosen so that there is only a few real-space vectors have to considered for the short range simulation. Unlike Ewald3D method, here the long range term separates the in-plane from the vertical components of the charge distances. The first term of the above equation is computed in real space while the second term undergoes many transformations and the final form of the potential can be written as:
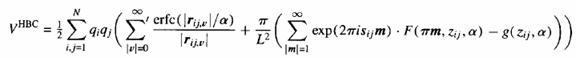
where
![]()
corrects for the inhomogeniety in the nonperiodic directions and
![]()
is the self energy term in the central sum that must be subtracted from the reciprocal space sum. z-dependence of the F function is an issue because Fourier part does not separate as well as in Ewald3D. In charge neutral systems when all the charges lie in a plane (zij=0) this method works well because F is simplified and g is zero. The complexity is O(N2). From a computational point of view this method is inconvenient.
De Leeuw and Perram (1979, 1980, 1983) used a different mathematical approach to come to the same conclusion as HBC.
Gryzybowski et al. (2000) uses the Poisson summation formula in 2 dimensions to get similar results as that of HBC but computationally this is expensive unless the lookup table method by Spohr (1994) is used.
Spohr et. al (1994) has showed that the calculation can be made more efficient by using a lookup table combined with an interpolation scheme and the long distance limit as z ->∞ where the distance between the periodic image is small compared to the distance between the sheets of charge. Then the force acting between two particles is given by
Fz= 2πq2/(LxLz)
Kawata and Mikami (2001) has come up with a method that is O(NxM) where M is the number of grid points in the z direction where they use a B-spline interpolation for the reciprocal space k=0 potential term.
The method of Hautman and Klein (HK)
Hautman and Klein (1992) considered the case in which the
deviation of the charge distribution from a purely two dimensional system is
small. For such a system one can introduce a
Super cell approximation with 3D Ewald
summation (EW3D)
Using the 3D Ewald sum by placing a slab of vacuum in between the periodic images would be another approach. Spohr (1994) and Yeh and Berkowitz (1997) have shown that even with a slab that is four times the distance between the charges one does not obtain the correct limiting behavior. This is because a periodically repeated slab behaves like a stack of parallel plate capacitors. If the slab has a net dipole moment, there will be spurious electric fields between the periodic image and the slab.
Correction to EW3D with extension in the
z direction (EW3DC)
Yeh and Berkowitz (1997) has shown that one can add a correction term to the 3D Ewald summation to obtain the correct limiting behavior in the limit of an infinitely thin slab. The potential
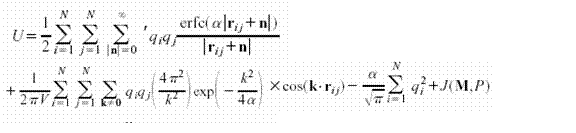
has a shape dependent term J (M,P) where M is the net dipole moment and P represents the geometry of the system. When the surrounding medium is vacuum this can be simplified as (Smith 1981)
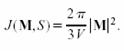
and the contribution to the force is
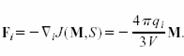
If a geometry of a rectangular plate or disk which are infinitely thin in the z direction are used as summation geometry in the Ewald Summation, then the shape dependent term J(M,R) is given by
![]()
Where, Mz is the z component of the total dipole moment of the simulation cell. This is equivalent of adopting a planewise sum method (summing x and y directions first then progressing in z direction (Hernando 1991)). Contribution to the force term is:
Our simulations show these corrected Ewald incorporated in GROMACS to work in conjunction with PME.
EW2D summation in conjunction with PME
O(NlnN)
While both approximate and rigorous Ewald summation techniques for surfaces and general nonperiodic systems have been described previously (HBC, HK) they are different from the standard Ewald summation that their adoption has not been widespread. The method of Yeh and Berkowitz (1999) is not exact 2 D summation but a correction to the 3D Ewald which works fine when sufficient vaccum ( at least 3 times the length in the periodic direction) is left in the non periodic direction. Minary et al (2002) proposes a new method that can be easily implemented on existing computer codes in conjunction with PME or SPME methods which is not a correction to the 3D Ewald but a rigorous 2D summation consisting of real and k space that is O(NlnN).The advantage is that no empty space is required in the nonperiodic direction. In their paper they provide equations which are a generalization of the standard Ewald sum. The differences from the standard Ewald sum include a slight modification of the background term and the addition of a screening function. Also, a second reciprocal space sum involving the out of plane structure factor and a corresponding modification of the full reciprocal space sum at zero in-plane reciprocal lattice vector is introduced. These modifications allow a spherical cut off of the reciprocal space to be employed in a standard way. Thus changes can be introduced into existing computer codes in conjunction with PME and SPME. Martyna and Tuckerman (1999) uses this approach for calculating long range interactions in clusters.
The advantage of using this approach over the lookup table method of Spohr (1994) is that existing codes for 3D systems which have Ewald 3D summation built in can be modified for 2D periodicity or 1D periodicity.
Simulations
Simulations were performed to compare EW2D (Analytical summation in 2D periodic systems), EW3D sum applied as a super cell approximation and the EW3DC with the correction term proposed by Yeh & Berkowitz.
The parameter α was chosen to be 0.3 Å-1. The cut off in real space and that in reciprocal space is 9.5 Å and 1.5 Å-1 respectively. Two systems were studied. Water confined between parallel plates and electrostatic interactions between two fixed charges both of which are 3D system with periodic boundary conditions in the third direction.
Water was confined between parallel plates at a constant density of 950 kg/m3, temperature of 300 K and at constant volume. SHAKE routine was used for rigidity of water. An electric field of 2V/A was applied in the x direction. Figure 6 shows the water density as a function of cross section for EW3D and EW3DC. The different is not much because the net dipole moment of the system in the z direction is approximately zero at equilibrium.
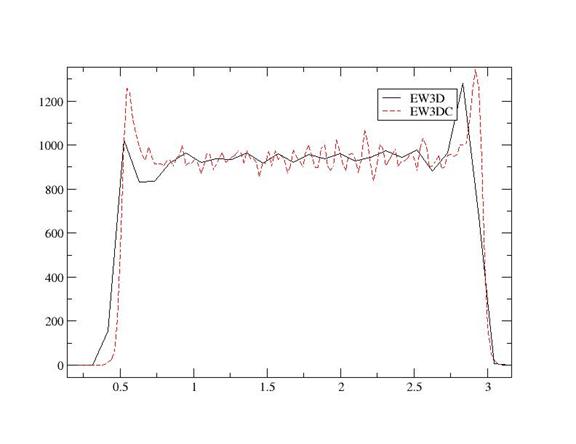
Figure 7: Water density as a function of cross section.
Another set of simulations were done with fixed particles of opposite charges with a box size of 18 Å x 18 Å x Lz Å where Lz varied as 18, 54 or 90. α was 0.45 and a reciprocal radius of 5 was used. The Lennard Jones potential was taken to be zero. The variation of forces with distance is shown for 3 cases.
Case 1: 2 oppositely charged particles at (0,0,0) and
(0,0,z) were z varied from 0 to Lz/2. 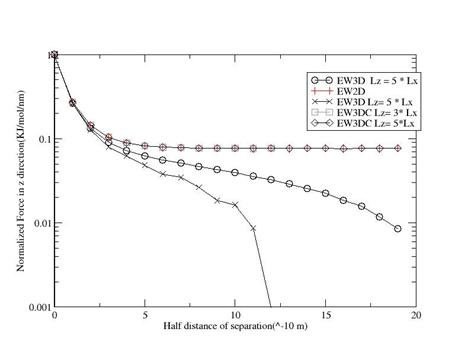
Figure 8
There is dipole moment only in the z direction. From the figure above it is seen that while the corrected Ewald 3D (EW3DC) matches with the 2D Ewald (EW2D) summation for Lz >=3*Lx, the Ewald3D (EW3D) deviates from the analytical expression (EW2D) even when Lz=5*Lx. The analytical values for EW2D was obtained from Yeh and Berkowitz and our simulation matches with Yeh and Berkowitz (1999).
Case 2: Two opposite charges at (0,0,0) and (4.5A,4.5A,z)
In this case there are dipole moments both in the x and y directions too. The results are shown below in Figure 8. There is excellent agreement of EW2D and EW3DC . This shows that even when dipole moment in x and y direction is not zero, the correction term involving dipole moment in z direction is sufficient.
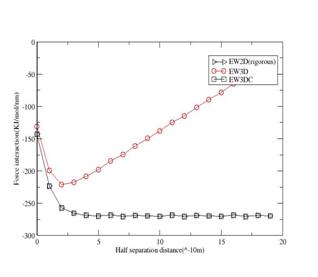
Figure 9
Case 3: 2 opposite charges at (0,0,z) and (0,0,-44A)
This is an extreme case where the charges are as far as possible from each other. EW3D with Lz=5*Lx deviates a lot from the EW2D. But EW3DC with Lz=5*Lx agrees well with EW2D except at short distances or very long distances (Yeh and Berkowitz 1999).
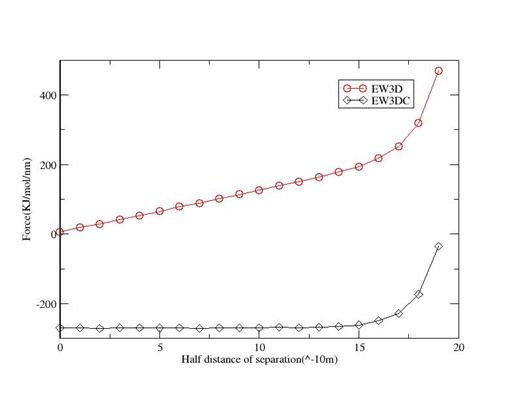
Figure 10
Conclusions and Future Work
We did a literature review for various methods for calculating short range and long range interactions especially those involving 2D periodic boundary conditions. We also compared using MD simulations, the super cell approximation and correction of Ewald 3D sum to subtract contributions from dipole moment in the non periodic direction. The results match well with previously published data.
As the next step, we have in mind implementing the algorithm by Minary et. al. for reduced periodicity systems in conjunction with PME which we couldn’t implement because of lack of time.
References
D. Frenkel & B. Smit, Understanding Molecular Simulations: Algorithms and Applications, Academic Press, 2002
Paul Gibbon, Godehard Sutmann, Long-Range Interactions in Many-Particle Simulation, published in Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms, Lecture Notes, J. Grotendorst, D. Marx, A. Muramatsu (Eds.),
John von Neumann Institute for Computing, Julich, NIC Series, Vol. 10, ISBN 3-00-009057-6, pp. 467-506, 2002.
E.L. Pollock and Jim Glosli, Comments on PPPM, FMM and the Ewald method for large periodic coulombic systems, Comput. Phys. Commun.,85,93 (1996)
E. R. Smith, Electrostatic Energy in Ionic crystals, Proc. Roy. Soc. London, Series A, Math. Phys. Sciences, Vol 375, 1763, pp. 475-505, 1981.
D. M. Heyes, M. Barber and J.H.R. Clark, Molecular dynamics computer simulation of surface properties of crystalline potassium chloride, J. Chem. Soc. Faraday Trans II, 73, pp 1485-1496, 1977.
L. Perera, U. Essmann and M.L. Berkowitz, Effect of the treatment of long range forces on the dynamics of ions in aqueous solutions, Journal of Chemical Physics, Vol 102(1), pp 450-456, 1995.
S. W. De Leeuw, J. W. Perram, and E. R. Smith,
Simulation of electrostatic systems in periodic boundary conditions. I.
Lattice sums and dielectric constants, Proc. Roy. Soc. Lon. 373,
27-56 (1980).
S. W.
De Leeuw, J. W. Perram, and E. R. Smith, Simulation of electrostatic systems
in periodic boundary conditions. II. Equivalence of boundary conditions,
Proc. Roy. Soc. Lon. 373, 57-66 (1980).
S. W. De Leeuw, J. W. Perram, and E. R. Smith,
Simulation of electrostatic systems in periodic boundary conditions. III.
Further theory and applications, Proc. Roy. Soc. Lon. 388,
1794, 177-193 (1983).
P. S. Crozier, R. L. Rowley, E. Spohr and D. Henderson. Comparison of charged sheets and corrected 3D Ewald calculations of long range forces in slab geometry electrolyte systems with solvent molecules. J. Chem. Phys., 112, pp 9253-9527, 2000.
G. J. Martyna and M. E. Tukerman, A reciprocal space based method for treating long range interactions in ab initio and force field based calculations in clusters, Journal of Chemical Physics, Vol 110, 6, pp 2810-2821, 1999
I. Yeh and M. L. Berkowitz, Ewald summation for systems with slab geometry, Journal of Chemical Physics, Vol 111,7, pp3155-3162, 1999.
A. Grzybowski, E. Gwozdz and A. Brodka, Ewald summation of electrostatic interactions in molecular dynamics of a three dimensional system with periodicity in two directions. Phys. Rev. B, 61, pp 67076-6712, 2000.
A. H. Widmann and D. B. Adolf. A comparison of Ewald summation techniques in for planar surfaces. Comput. Phys. Commun., 107:167-186,1997.
S. W. de Leeu and J. W. Perram. Electrostatic lattice sums for semi-infinite lattices. Mol. Phys. 37. pp 1313-1322, 1979.
E. Spohr. Effect of boundary conditions and system size on the interfacial properties of water and aqueous solutions. J. Chem. Phys., 107, pp 6342-6348. 1994
P. Minary, M. E. Tukerman, K. A. Pihakari, G. J. Martyna, A new reciprocal space based treatment of long range interactions on surfaces , J. Chem. Phys, 116, 13, 2002.
M. Kawata and M. Mikami,
Rapid calculation of 2D Ewald Sums,
Chem. Phys. Letters,
340, 157-164, 2001.
J. A. Hernando, Multipolar electrostatic sums in numerical simulations with wall boundary conditions, Physical Review A, 44 (2), 1228-1232, 1991.
J. Hautman and M.L. Klein, An Ewald summation method for planar surfaces and interfaces, Mol. Phys. 75, pp 379-395, 1992.