Results:
 

For each set of parameters (Nc, P), the growth radii Rg, Rmax­, and the fractal dimension d are measured.  We run the program 10 times (with different random number seeds) to obtain the error bars. Each run takes 2000 time steps.

Patterns:

 

We grow the bacterial colonies in different conditions:
 

1. One inoculation points at the center (100,100)

(a) Fixed surface roughness Nc=6

Vary initial nutrient concentration P= 9.0, 7.0, 5.0, 3.0, and 1.0.
 
 


 
 








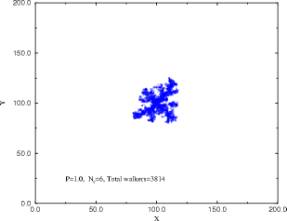
Obviously, as the nutrient concentration decrease from 9.0 to 1.0, not only does the growth radius decrease sharply, but also the structure changes from highly compact to ramified and branching. Also, the number of walkers in the final stage (after 2000 steps) decreases from 105 to 103.This is typical behavior for a diffusion-limited process, as has been observed in many living and non-living systems. The bacteria interact locally through nutrient consumption and in starvation conditions tend to branch to reach the optimal amount of food.We shall see in the following dimensional analysis how the fractal dimension depends on the availability of the nutrient.
 
 

(b) Fixed initial nutrient concentration P=2.0

Varying surface roughness Nc=2, 4, 6, 8 and10
 
 


 
 


 
 





As expected, the growth radius decreases with increasing surface roughness, since more efforts are need to push the envelope and lubricate unoccupied space.  However, the fractal dimension does not seem to change too much with the roughness, as seen from the similarity between the four patterns generated from different Nc. Also, the total number of walkers in the final stage is almost in the same order, in contrast to the sharp change when the nutrient concentration is varied with fixed surface roughness. Since the initial nutrient level is fixed at P=2.0, which is not high, we don?t see compact (dimension=2) patterns even on very smooth surfaces.
 
 

2. Two innoculation points at different locations

(a)Nc=6, p=5.0;

Inoculation points (40,100) and (160,100), Dd=80
 
 





At large distance, Dd=80, the two colonies grow almost independently and the generated patterns are just like individual ones.
 

(b)Nc=6, p=5.0;
Inoculation points (75,100) and (125,100), Dd=50

 





When the two colonies are brought to close enough to each other, they begin to compete with for the food. The pattern above shows that a wide gap exists between the patterns generated by two colonies. Instead of running into their cousins, they tend to grow in the opposite direction and keep a distance from their competitors.It is interesting to make the analogy between the interactions of two bacterial colonies and the coulomb interaction between two disk capacitors with like charges. When the two capacitors are far enough apart, the charges are just evenly distributed on the disk surface. With decreasing distance, the charges on the two disks repel each other and tend to flow into the opposite side. Here the two bacterial colonies behave just like there is an expelling force between them. However, the interaction is not from a simple force, but is indirectly associated with the competition for food.
 
 

Growth radius Rg,Rmax:

We measure the growth radius Rg (defined as squared averaged radius ) and Rmax for each set of parameters.
 

(1)Fixed roughness Nc=6




 
 
 

(2)Fixed initial nutrient concentration.





The tendency of the change of growth radius is as expected and the error of the estimated average of each data set are reasonably small, which confirms the robustness of the growth algorithm in our program. The maximum radius is almost twice the gyration radius Rg, while for evenly distributed round disk, the expected ratio is .  The difference in the ratio is not simply caused by the fact that the fractal dimension of the bacterial colonies is less than 2, but also by the high concentration of walkers in the center due to the initial innoculation. If instead, we release the initial walkers from the edge and let them move randomly until sticking to some fictitious attracting center, the ratio of Rmax over Rg might represent the fractal effect more realistically.
 
 

Fractal dimension:
 

Due to the high concentration in the innoculation center and the compactness of the growth radius at low concentration or high roughness, the measurement of the fractal dimension is less smooth than those of the radius.
 

(1)Fixed roughness Nc=6


First we notice the difference of fractal dimension yielded by the two methods, i.e., the mass distribution method and the box counting method. By comparing the data with the patterns, we find that the latter is more reliable in our case. As explained before, the systematic error of the mass distribution method here is caused by the high concentration of walkers in the center. However, we can see the tendency of fractal dimension in both curves. As the nutrient concentration increases, the structure grows more and more compact. As we expect, when P tends to infinity, the fractal dimension saturates at 2.
The error bars are large at low concentration because in that case the gyration radius is small(<20) and we have only a few shells of mass distribution to fit the dimension. We have the same problem with the box counting method, but since the number of blocking size is dependent on Rmax and not Rg, we always have more data points for fitting than with the mass distribution method.Thus, the deviations are smaller.

 
 
 
(2)Fixed initial nutrient concentration P=2.0





Both curves show that the fractal dimension is not strongly dependent on the surface roughness, which does not agree with the experimental observations that the patterns become more ramified at harder agar surface. One possible reason is that in our simulation, the surface hardness is not high enough to see substantial changes in the dimension. The 2000 steps take about 8 minutes on a workstation, and if we can make our codes run faster, it is possible to grow the same size of bacterial colonies on extreme hard surfaces and analyze the dimensional dependence on Nc.