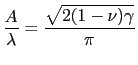Shear Properties and Wrinkling Behaviors of Finite Sized Graphene
Kyoungmin Min, Namjung Kim and Ravi Bhadauria
MSE485 Atomic Scale Simulation
11 May 2010
In this project, we investigate the shear properties of finite sized graphene under direct shear loading conditions. The shear properties calculated with the simulations show size dependency but little chirality effects. Other objective of the project was to investigate the wrinkling behavior under shear conditions. However, due to the finite size, comparisons with theory could not be made correctly.
Graphene is a single layer of sp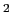 hybridized carbon atoms that are arranged in a hexagonal lattice of honeycomb shape. It has gained much attention recently because of its many potential applications, viz. detecting single molecule gas [1], transistors, novel capacitors, transparent conducting electrodes etc. Apart from above mentioned areas, significant amount of fundamental research is dedicated towards understanding mechanical properties of graphene suited for various purposes; where researchers [2] have concluded in their experiments that graphene is one of the strongest material with breaking strength of 130 GPa, and has a Young's modulus of 1.0 TPa. Using atomic force microscopy, some experiments have been performed to study the spring constant of graphene where it was found that the spring constant of graphene is in range of 1-5 N/m, which makes it very useful for NEMS applications such as pressure sensors and resonators [3].
hybridized carbon atoms that are arranged in a hexagonal lattice of honeycomb shape. It has gained much attention recently because of its many potential applications, viz. detecting single molecule gas [1], transistors, novel capacitors, transparent conducting electrodes etc. Apart from above mentioned areas, significant amount of fundamental research is dedicated towards understanding mechanical properties of graphene suited for various purposes; where researchers [2] have concluded in their experiments that graphene is one of the strongest material with breaking strength of 130 GPa, and has a Young's modulus of 1.0 TPa. Using atomic force microscopy, some experiments have been performed to study the spring constant of graphene where it was found that the spring constant of graphene is in range of 1-5 N/m, which makes it very useful for NEMS applications such as pressure sensors and resonators [3].
Graphene, with many other materials at nanoscale level, are subject to thermal and quantum fluctuations which result into inherent rippling or wrinkling phenomenon. It has been seen that although the amplitude of these fluctuations is bounded in 3D structures, theory suggests that the disturbance will grow logarithmically from finite 2D to infinite 2D size, and would be unbounded for the latter. Ripples in suspended graphene nanolayers have been previously observed [4] and researchers have attributed these properties to thermal fluctuations. However, under the action of a lateral stress, this phenomenon is less likely to observe.
Recently, elastic properties of finite sized graphene sheet have been calculated [5]. One of the ways to compute the properties is by using molecular structural mechanics method [6]. In this method, carbon atoms have been modeled as equivalent space frame structures, with their interaction incorporated as an equivalent structural beam. This approach is more analytical in nature and out of plane effects are neglected. To understand the complete physics while investigating the properties, density functional theory methods have been employed to simulate planar graphene nanoribbons, whose elastic modulus is considerably higher than infinitely long graphene [7]. Finite sized planar graphene nanoribbon has two configurations, namely zigzag and armchair which have different mechanical properties [8]. Although tension test simulations have been performed [8,9], almost negligible effort has been made to study the shear properties using molecular dynamics for finite size graphene, which will help resolving the buckling or wrinkling phenomenon [10].Hence, it is necessary to understand the properties of graphene for different finite sizes and chiralities using atomic scale calculations.
The shear properties of finite sized planar graphene nanoribbon were of primary interest, and a proper boundary condition for applying the strain was required. To resolve this, three different types of boundary conditions in which (a) strain was applied directly to the model, (b) boundary atoms are displaced and ensuing structure is relaxed, (c) velocity boundary condition is applied to top atoms. Both chiral configurations will be tested for shear strength. AIREBO potential [11] was used for molecular interaction since it allows for covalent bond breaking and creation with associated changes in atomic hybridization within a classical potential. It was chosen over Tersoff's potential since the latter does not allow torsion. LAMMPS [12] was used as molecular dynamics engine. The Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential [11] computes the potential for a system of carbon and/or hydrogen atoms. The potential consists of three terms:
![$\displaystyle E = \frac{1}{2} \sum_i \sum_{j \neq i} \left[ E_{ij}^{REBO} + E_{ij}^{LJ} + \sum_{k \neq i,j} \sum_{l \neq i,j,k} E_{ijkl}^{TORSION} \right]$](img2.png) |
(1) |
All three terms are included in the calculation. The first term is the REBO potential first introduced by Brenner et al. [13]. The second term incorporates longer-ranged interactions using a form similar to the Lennard Jones potential, which the third term includes torsion; it is a four body potential that describes various dihedral angle preferences in hydrocarbon configurations. A NVT ensemble at 300K was used in all simulations. Nose-Hoover thermostat was used to maintain temperature. In MD simulation, it is important to find the optimized values for MD input to achieve the reliable results. Several simulations were performed to find parameters which show the stable and reliable results. The number of atoms ranged from 72 to 836. Time step of 0.1 fs was chosen for numerical integration using velocity verlet algorithm, and the structure was relaxed for 1 ps. After the energy minimization, shear strain was applied. Bottom atom layer was fixed and top atom layer was displaced with 0.05 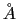 and relaxed 10 ps for relaxation for the applied strain. For boundary condition (a), results were similar to that of (b) and applying (c) resulted in unstable simulation. Hence all the calculations were performed with (b) condition since it is easier to implement.
and relaxed 10 ps for relaxation for the applied strain. For boundary condition (a), results were similar to that of (b) and applying (c) resulted in unstable simulation. Hence all the calculations were performed with (b) condition since it is easier to implement.
In the following subsections, various results would be discussed.
As seen from the figure 1, temperature, pressure, and potential energy reached at the stable values roughly after 400 steps. Figure 2 displays variation in thermodynamic properties for increasing shear load case of 364 atoms. The shear load is increased till fracture occurs. Temperature, potential energy, and pressure show sudden change in values to corroborate the fracture phenomenon.
Figure 1:
Plot of Temperature, Pressure and Potential Energy of the structure during relaxation
![\includegraphics[scale=0.7]{mdverrlx.eps}](img4.png) |
Figure 2:
Plot of Temperature, Pressure and Potential Energy of the structure under shear load
![\includegraphics[scale=0.7]{mdvershr.eps}](img5.png) |
Figure 3 shows shear stress and strain curve for different size and chirality. For small number of atoms (72), zigzag configuration can hold more for shear load than armchair. For 576 atoms, which is towards the infinite 2D limit, there is no significant chirality effect. As the size of structure increases, it can hold more shear stress and strain.
Figure 3:
Plot of shear stress versus shear strain for different size and chirality
![\includegraphics[scale=0.7]{strs_strn.eps}](img6.png) |
Shear properties such as shear modulus, shear strength and fracture shear strain for different sizes and chiralities were calculated. As seen from figure 4, for small size of finite graphene sheet, small chirality effect is observed which converges asymptotically to bulk value (Shear modulus = 450 GPa (Armchair), 480 GPa (Zigzag), Shear strength = 60 GPa) [14] as the size of the structure is increased. It is because at the small size, the edge effect is easily induced to the structure which influences the behavior of the different chiral structures. However, there is no chirality effect for shear properties for large size cases. There is possibility that if sizes are further increased, then the chirality effect would be more pronounced once its values are closer to the bulk. But in the range of size that was covered, any significant effect was not captured.
Figure 4:
Shear properties for different chirality and size
![\includegraphics[scale=0.7]{shprop.eps}](img7.png) |
To quantify the wrinkling phenomenon, Wong and Pellegrino [10] did systematical and extensive studies about wrinkle behaviors of membrane under shear using analytical, experimental, and simulations, where they proposed a formula for calculating ratio of amplitude and half-wavelength which is
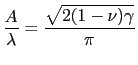 |
(2) |
where 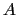 is the amplitude of the disturbance,
is the amplitude of the disturbance, 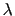 is the half wavelength,
is the half wavelength, 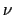 is the Poisson's ratio and
is the Poisson's ratio and 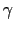 is the shear strain. Value of Poisson's ratio is taken from a published work of one of the team member [9] and the values are summarized in Table 1. Figure 5 shows the result based on present simulations. Since the equation is function of poisson's ratio, it is important to calculate the poisson's ratio correctly. We use the data presented in Table 1 which used the AIREBO potential for finite size. From the figure, it can be summarized that there is no chirality effect on the ratio, but a significant increase is observed with increasing size.
is the shear strain. Value of Poisson's ratio is taken from a published work of one of the team member [9] and the values are summarized in Table 1. Figure 5 shows the result based on present simulations. Since the equation is function of poisson's ratio, it is important to calculate the poisson's ratio correctly. We use the data presented in Table 1 which used the AIREBO potential for finite size. From the figure, it can be summarized that there is no chirality effect on the ratio, but a significant increase is observed with increasing size.
Table 1:
Poisson's ratio for Armchair and Zigzag configurations
| No. Atoms |
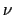 (Armchair) (Armchair) |
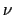 (Zigzag) (Zigzag) |
| 72 |
0.270766 |
0.270766 |
| 180 |
0.272553 |
0.256468 |
| 364 |
0.257362 |
0.239489 |
| 576 |
0.243957 |
0.225191 |
| 836 |
0.240383 |
0.224298 |
|
Figure 5:
Ratio of amplitude and half wavelength for different size and chirality
![\includegraphics[scale=0.7]{ampwave.eps}](img13.png) |
The goal was to quantify wrinkle behavior and compare it to the analytical expression for the verification. However, there were some problems because of the finite size. In the snapshot of armchair and zigzag configuration for 836 atoms (largest case) shown in Figures 6 and 7, the wrinkles are clearly generated to the diagonal direction where the compression force is induced due to the shear load. However, looking at snapshot of wrinkle view, one can see that it is not certain which value of wavelength and amplitude should be taken into consideration due to the edge effect. Smaller sizes show even bigger disparity in the edge and the interior values. If the number of atoms are increased sufficiently to the infinite case, then the edge effect will be minor and probably a correct comparison could be possible. Since the CPU time of performing simulation were expensive, investigation upto 836 atoms was feasible and hence performed in the present study.
Figure 6:
Rippling in Armchair configuration
![\includegraphics[scale=0.7]{ACcood.eps}](img14.png) |
Figure 7:
Rippling in Zigzag configuration
![\includegraphics[scale=0.7]{ZZcood.eps}](img15.png) |
In this project, effort has been made to study the shear properties and wrinkling behavior of finite size graphene. Shear modulus, shear strength and shear strain depend directly on the size of the graphene ribbon, and they increase towards the infinite 2D value. Chirality was shown not to be a important factor in the finite size regime. Along with that, wrinkle behavior from theoretical formulations could not be verified for finite sized graphne due to the edge effects. If the size of the graphene is increased, it is expected that the result would be closer to the ones predicted from theory and calculations for infinitely long 2D graphene.
- 1
-
F. Schedin et al., Nature Materials, Vol. 6, pp. 652-655 (2007)
- 2
-
C. Lee et al., Science, Vol. 321, No. 5887, pp. 385-388 (2008)
- 3
-
I. W. Frank et al., Journal of Vacuum Science and Technology B, Vol. 25, No. 6, pp. 2558-2561 (2007)
- 4
-
J. Meyer et al., Nature, Vol. 446, pp. 60-63 (2007)
- 5
-
A. Sakhaee-Pour, Solid State Communications, Vol. 149, No. 1-2, pp. 91-95 (2009)
- 6
-
C. Li and T.W. Chou, International Journal of Solids and Structures, Vol. 40, No. 10, pp. 2487-2499 (2003)
- 7
-
R. Faccio et al., Journal of Physics: Condensed Matter, Vol. 21, No. 28, pp. 5304-5310 (2009)
- 8
-
H. Bu et al., Physics Letters A, Vol. 373, No. 37, pp. 3359-3362 (2009)
- 9
-
H. Zhao et al., Nano Letters, Vol. 9, No. 8, pp. 3012-3015 (2009)
- 10
-
Y. W. Wong and S. Pellegrino, Journal of Mechanics of Materials and Structures, Vol. 1, No. 1, pp. 27-61 (2006)
- 11
-
S. Stuart et al., Journal of Chemical Physics, Vol. 112, No. 14, pp. 6472-6486 (2000)
- 12
-
S. J. Plimpton, Journal of Computational Physics, Vol. 117, pp. 1-19 (1995); http://lammps.sandia.gov
- 13
-
D. W. Brenner et al., Journal of Physics: Condensed Matter, Vol. 14, No. 4, pp. 783-802 (2002)
- 14
-
K. Min and N. R. Aluru, In preparation (2010)
Shear Properties and Wrinkling Behaviors of Finite Sized Graphene
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons report report.tex
The translation was initiated by Ravi Bhadauria on 2010-05-10
Ravi Bhadauria
2010-05-10
![$\displaystyle E = \frac{1}{2} \sum_i \sum_{j \neq i} \left[ E_{ij}^{REBO} + E_{ij}^{LJ} + \sum_{k \neq i,j} \sum_{l \neq i,j,k} E_{ijkl}^{TORSION} \right]$](img2.png)
![]() and relaxed 10 ps for relaxation for the applied strain. For boundary condition (a), results were similar to that of (b) and applying (c) resulted in unstable simulation. Hence all the calculations were performed with (b) condition since it is easier to implement.
and relaxed 10 ps for relaxation for the applied strain. For boundary condition (a), results were similar to that of (b) and applying (c) resulted in unstable simulation. Hence all the calculations were performed with (b) condition since it is easier to implement.