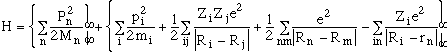
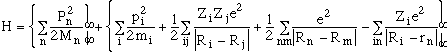
Interatomic Potentials from Born-Oppenheimer Approximation

Ultimately, a system of interacting atoms, molecules, etc., are composed of electons and nuclei which interact with one another to produce the macroscopic behavior. With the notation that n or m refer to electrons (with electric charge, mass, position and momenta, e, m, r and p, resp.) and i or j refer to nuclei (with atomic number, mass, position and momenta, Z, M, R and P, resp.), we may write the Hamiltonian for this system as a sum of these two contributions, H= H_nuclei + H_electrons , i.e.,

where the kinetic energies and potential energies are apparent. In principle, one should solve the Schrodinger or Dirac equations (e.g., Hy(r_n,R_i) = Ey(r_n,R_i)) for the system wavefunction y(r_n, R_i) and we have an exact solution. Note that, in general, r_i are generalized coordinates which may be the position of the atoms or for rigid-rotating molecules, for example, they would be center-of-mass coordinates and molecular orientation, and so on. The Kinetic energy usually has the form of p_i²/2m_i. (see A&T pg. 6 section 1.3)

Because the mass of the electron relative to the nuclei is small, or M/m= 100-1000, and the respective frequencies (inverse of the time, t) of response are w_e/w_nucl = t_nucl/t _e= M/m, Born and Oppenheimer in 1923 suggested that one could represent the wavefunction as a product, i.e. y (r_n,R_i)= X(R_i)f(r_n; R_i). In effect, this just says that the nuclei move much more slowly than the electrons (and are more or less fixed as the electrons equilibriate). Notice that the electron wavefunction depends on the position of the nuclei parameterically. As a result of this product wavefunction, the problem breaks up into the separate equations to solve.

The electrons equations is H_el f(r_n; R_i)= V(R_i)f(r_n; R_i). The equation for the atomic nuclei (using the effective interatomic potentials V(R_i) which is given in the second set of brackets above) is given by

,
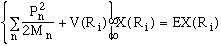which does not depend on the electronic degrees of freedom at all. Therefore, it is traditional to solve this Shrodinger equation classically using Newton's equations. This is, of course, only valid if the de Broglie thermal wavelength, L, is much less than a nearest neighbor separation, a. For light elements, L/a= 0.1 and gets smaller for larger nuclei. For lighter elements or molecules, such as He or H₂, this breaks down and quantum corrections are required.

Back