PHYS 150 :: Physics Illinois :: University of Illinois at Urbana-Champaign
Core Math
Scientific notation
This course will take us from the scale of atoms to that of the universe. Along the way we'll encounter many numbers that are much larger are smaller than those from everyday experience. When dealing with very large or very small numbers, it is much more convenient (and takes a lot less typing) to use scientific notation. Scientific notation takes the form 
and the rule is quite simple:
- If n is positive, move the decimal point n places to the right.
- If n is negative, move the decimal point n places to the left.
. Many calculators also use this notation. Some examples:
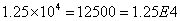
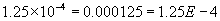
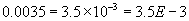
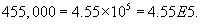
Algebra
We will use the following notation:
means "x plus y"
means "x minus y"
means "x times y"
means "x divided by y"
means "x to the y power" or "x times itself y times"
Example:
means "the square root of x" and 
Geometry and Trigonometry
The figure shows a right triangle. It is a right triangle because one of the angles is 
The other two angles are 
and the sides have length a, b, and c.
We have the following relationships:
Pythagorean Theorem: 
Sine is opposite over hypotenuse: 
and 
Cosine is adjacent over hypotenuse: 
and 
Tangent is opposite over adjacent: 
and 
Prefixes
When discussing big or small numbers we'll sometimes use SI prefixes on units of measurement. Common examples include "kilometer" (instead of 103 meters), "milligram" (instead of 10-3 grams), "gigawatt" (instead of 109 watts), etc. I've listed them all below - we'll only need the first few rows!
| 1e-3 | milli- (m) | 1e3 | kilo- (k) | |
| 1e-6 | micro- (μ) | 1e6 | mega- (M) | |
| 1e-9 | nano- (n) | 1e9 | giga- (G) | |
| 1e-12 | pico- (p) | 1e12 | tera- (T) | |
| 1e-15 | femto- (f) | 1e15 | peta- (P) | |
| 1e-18 | atto- (a) | 1e18 | exa- (E) | |
| 1e-21 | zepto- (z) | 1e21 | zetta- (Z) | |
| 1e-24 | yocto- (y) | 1e24 | yotta- (Y) |