

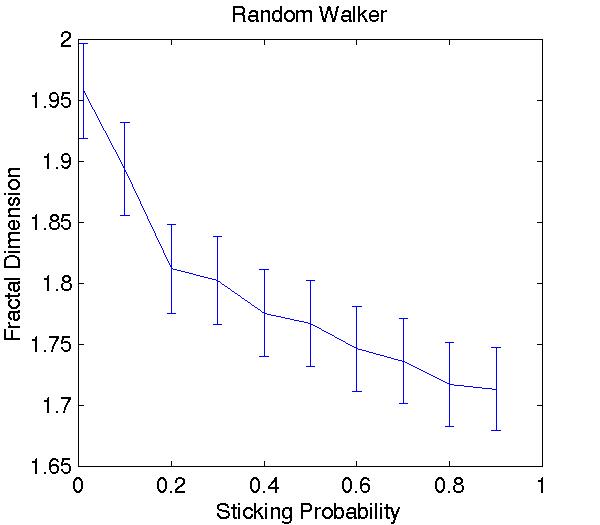
Both show the expected downward trend as the forms become more fibrous and open as well as the limiting value of 2 for the compact limit. As the interaction range is increased the landscape is depleted for a large distance around the growing dendrite. It is therefore favorable for the dendrites to be widely spaced and produce an open pattern.. Likewise, a high sticking probability allows particles to adhere quickly so produce a branched, open structure, while a low sticking probability allows much diffusion after primary impacts, producing a compact pattern.
There is a clear difference in the concavity of the curves. As the interaction range for the active walker increases, its fractal dimension quickly falls off. Presumably it eventually approaches 1, the limit for a linear form. The random walker, however, approaches a much higher limiting value around 1.7. This would seem to indicate that their is some minimum size for local particle agglomerates to be stable, while crystals may grow into extremely thin needles as is often observed.
One of our group members (Dapeng Guan) has developed a somewhat more detailed explanation for the decrease of the fractal dimension with increasing interaction. To access it click here.