

Next: About this document ...
Up: Local Energy Calculation of
Previous: Jastro correlation factor
In this section, we explicity compute the gradient and Laplacian of the
determinant of the trial wave function. In particular, we seek
![\begin{displaymath}\nabla [\ln \det(A)],
\end{displaymath}](img54.gif) |
(19) |
where A is either the up or down matrix. To simplify
the analysis, we will initially work again in terms of components.
Let
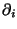 represent the derivative with respect to a single
component of the 3N dimensional
R. Trivially, then,
represent the derivative with respect to a single
component of the 3N dimensional
R. Trivially, then,
![\begin{displaymath}\partial_i \ln[\det(A)] = \frac{1}{\det A} \partial_i \det (A)
\end{displaymath}](img56.gif) |
(20) |
At first glance, taking the derivative of a determinant appears a
daunting task. Considerable simplification is possible with the
following simple relation, which we state without proof:
![\begin{displaymath}\partial_i \det(A) = \det(A) \,\text{Tr}\,[A^{-1} \partial_i A]
\end{displaymath}](img57.gif) |
(21) |
Then
![\begin{displaymath}\partial_i \ln [\det(A)] = \,\text{Tr}\,[A^{-1} \partial_i A]
\end{displaymath}](img58.gif) |
(22) |
Given this form, we are left with the calculation of the the elements
of
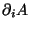 .
The elements of A are just
.
The elements of A are just
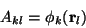 |
(23) |
It is quite easy to see that the elements of the derivative matrix will
be zero unless
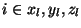 .
Then the derivative matrix will
have a single non-zero column. By taking advantage of symmetry, we can
calculate the x, y, and z components simultaneously by directly
calculating
.
Then the derivative matrix will
have a single non-zero column. By taking advantage of symmetry, we can
calculate the x, y, and z components simultaneously by directly
calculating
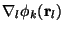 .
If we make the substitution,
.
If we make the substitution,
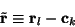 |
(24) |
then
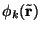 will be radially symmetric in
will be radially symmetric in
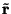 .
Since
these vector operators are translationally invariant,
.
Since
these vector operators are translationally invariant,
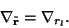 |
(25) |
If we work in spherical coordinates,
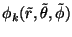 will be independent of
will be independent of
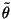 and
and
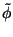 .
We can then express the gradient as
.
We can then express the gradient as
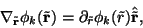 |
(26) |
where
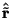 represent the unit vector in the direction of
represent the unit vector in the direction of
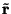 .
Written in terms of
.
Written in terms of
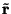 ,
the orbitals take the form,
,
the orbitals take the form,
 |
(27) |
The derivative takes the form
and furthermore,
The total Laplacian will be a sum of the Laplacian's with respect to
each electronic coordinate,
ri. Let i represent a particular
component of the 3N dimensional vector,
R, eg. the x component
of
r4. Then we have that
where
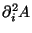 actually denotes the Laplacian of the components
of the matrix A.
For the latter term, we utilize the fundamental property of inverses,
actually denotes the Laplacian of the components
of the matrix A.
For the latter term, we utilize the fundamental property of inverses,
Using this new relation
Now, to calculate the Laplacian with respect to
rm, we sum over
the three components, j, of the
rm.
![\begin{displaymath}\nabla^2_{{\mathbf r}_m} \ln[\det(A)] = \,\text{Tr}\,[A^{-1} ...
...,z\}} \,\text{Tr}\,[(A^{-1}(\partial_{{\mathbf r}_m^j} A))^2],
\end{displaymath}](img94.gif) |
(33) |
where
rmj refers to the
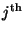 component of
rm.
component of
rm.
We already have the first derivative of A, which we found in the
gradient part of the calculation. Next we calculate the Laplacian
of the compoents of A. Specifically, we seek
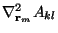 ,
where
,
where
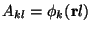 .
We have that
.
We have that
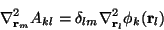 |
(34) |
What remains is the Laplacian of the molecular orbitals, 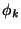 ,
with
respect to
rl. If we make the definition,
,
with
respect to
rl. If we make the definition,
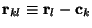 ,
we recognize that
,
we recognize that
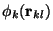 will
spherically symmetric. Differential operators are invariant under
translations, so we simplify the calculation our calculation by
exploiting this translational invariance
will
spherically symmetric. Differential operators are invariant under
translations, so we simplify the calculation our calculation by
exploiting this translational invariance
The first derivative of the molecular orbitals were computed earlier in
this paper, so we finally turn to computing the second derivative of the
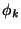 's.
's.


Next: About this document ...
Up: Local Energy Calculation of
Previous: Jastro correlation factor
Nichols A. Romero
1999-12-17
![$\displaystyle \phi_k(\tilde{r}) \partial_{\tilde{r}} \left[
\frac{- \tilde{r}^2}{\omega_k^2 + \nu_k \tilde{r}}\right]$](img74.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[\frac{-2 \tilde{r}}{\omega_k^2 + \nu_k \tilde{r}} +
\frac{\nu_k \tilde{r}^2}{(\omega_k^2 + \nu_k \tilde{r})^2} \right]$](img75.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[\frac{-2\tilde{r}(\omega^2 + \nu_k \tilde{r}) + \nu_k \tilde{r}^2}
{(\omega_k^2 + \nu_k)^2} \right]$](img76.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[ \frac{ -\tilde{r}(2\omega_k^2 + \nu_k
\tilde{r})}{(\omega_k^2 + \nu_k \tilde{r})^2} \right]$](img77.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[ \frac{ -\tilde{r}(2\omega_k^2 + \nu_k
\tilde{r})}{(\omega_k^2 + \nu_k \tilde{r})^2} \right] \hat{\tilde{{\mathbf r}}}$](img79.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[ \frac{ -\tilde{r}(2\omega_k^2 + \nu_k
\t...
...k \tilde{r})^2} \right] \left(\frac{{\mathbf r}-
{\mathbf c}}{\tilde{r}}\right)$](img80.gif)
![$\displaystyle \phi_k(\tilde{r}) \left[ \frac{ -(2\omega_k^2 + \nu_k
\tilde{r})}{(\omega_k^2 + \nu_k \tilde{r})^2} \right] ({\mathbf r}- {\mathbf c}).$](img81.gif)
![]() ,
where
,
where
![]() .
We have that
.
We have that
![]() 's.
's.
![$\displaystyle \partial_{\tilde{r}}
\phi_k(\tilde{r}) \left[ \frac{ -\tilde{r}(2\omega_k^2 + \nu_k \tilde{r})}{(\omega_k^2 +
\nu_k \tilde{r})^2} \right]$](img105.gif)
![$\displaystyle \left[ \frac{ -\tilde{r}(2\omega_k^2 + \nu_k \tilde{r})}{(\omega_...
...de{r}(2\omega_k^2 + \nu_k \tilde{r})}{(\omega_k^2 +
\nu_k \tilde{r})^2} \right]$](img106.gif)
![$\displaystyle \phi_k(\tilde{r}) \frac{\left[\tilde{r}(2\omega_k^2 + \nu_k \tilde{r})\right]^2}{(\omega_k^2 + \nu_k \tilde{r})^4}$](img107.gif)
![$\displaystyle - 2 \phi_k(\tilde{r}) \left[\frac{(\omega_k^2 + \nu_k \tilde{r})^...
...de{r})(2\omega_k^2 + \nu_k \tilde{r})}{(\omega_k^2 + \nu_k \tilde{r})^4}\right]$](img108.gif)