Introduction

Mass transport due to the coupling of temperature and concentration fields was first introduced by Ludwig in 1856  [2]. Since this time several others have conducted experiments supporting such phenomena. Even though nearly 150 years has passed, thermal diffusion or the (Ludwig - Soret effect) is still poorly understood at the microscopic level and an accepted theory doesn't exist. Today technical advances have made it possible to conduct more accurate experiments and computer simulations. In addition, modern advances have given birth to new applications of thermal diffusion in processes such as isotope separation and chemical vapor deposition  [13].
In general, complicated situations involving multicomponent systems (where more than two fluxes and associated forces exist) are generalized by Onsager's linear relationship,

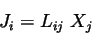$$J_{i} = L_{ij} \ X_{j}$$ (1)

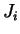where $J_{i}$ is the flux of component i and 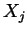$X_{j}$ are the corresponding thermodynamic forces. In binary systems dealing with the thermodynamic forces of temperature and concentration gradients equation(1) above reduces to

$$J_{1} = -D_{12}\left[\left(\frac{\partial{x_{1}}}{\partial{... ...(1-x_{1})\left(\frac{\partial{T}}{\partial{z}}\right)\right]$$ (2)

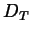where the temperature gradient is limited to z axis. Above $S_{T}= \frac{D_{T}}{D_{12}}$ is defined as the Soret coefficient and is a measure of the relative coupling between the diffusion induced by the temperature field $D_{T}$ and the Fickian diffusion driven by the concentration field (also known as the mutual diffusion coefficient 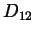$D_{12}$). In general, if a temperature gradient is maintained the system will enter a nonequilibrium steady state such that the mass flux is zero and the heat flux is constant. In this special case  [2], equation(2) can be reduced to,

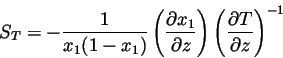$$S_{T} = - \frac{1}{x_{1}(1-x_{1})}\left( \frac{\partial{x_{... ...}}\right) \left( \frac{\partial{T}}{\partial{z}}\right)^{-1}$$ (3)

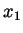where $x_{1}$ is the molar fraction of component 1.
To our knowledge, prior to the paper only MD simulations have been developed to study the (Ludwig-Soret) effect. This may be due to the fact that the several MD techniques as well as ours suffer from both conceptual and physical problems. For example, how is the heat and mass transfer accurately defined in a simulation. And most importantly, the methods have required completely unphysical perturbation fields, on the order of 1 degree Kelvin per lattice site.