


Next: Driven KMC Algorithm
Up: Methods
Previous: Methods
Figure 1:
1 dimensional representation of the potential energy surface. 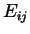 is the energy barrier between the two states
is the energy barrier between the two states 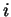 and
and 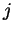 .
.
|
|
Our approach follows the same methodology provided by D. N. Theodorou et al. [6] and K. A. Fichthorn et al. [9]. We take a similar approach in solving for the rate constants
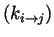 in the Markovian Master equation,
in the Markovian Master equation,
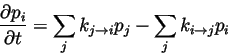 |
(4) |
where the rate constants shown in equation(5) below
![\begin{displaymath}
k_{i\rightarrow j} = \nu_{i} \ e^{\left[-\frac{E_{i j} - E_{i}}{k_{b} T_{i}}\right]}
\end{displaymath}](img19.gif) |
(5) |
are obtained via the application of the Arrhenius Law in Transition State Theory (TST). Of most importance is the energy barrier (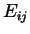 ) between the vacancy state (j) and the diffusive atoms state (i). Figure(1) above displays a fictitious potential energy for a diffusing atom in 1 dimension.
In a majority of the past simulations that apply (TST) to KMC methods the frequency factor
) between the vacancy state (j) and the diffusive atoms state (i). Figure(1) above displays a fictitious potential energy for a diffusing atom in 1 dimension.
In a majority of the past simulations that apply (TST) to KMC methods the frequency factor 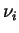 is assumed to be a constant. In general
is assumed to be a constant. In general 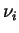 is of the form,
is of the form,
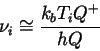 |
(6) |
where 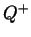 is the partition function of the transition state and
is the partition function of the transition state and 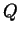 is the partition function of the reactant state. A major concern in our simulation was whether or not the local rate constants could be considered a function of the local temperature, and if so is this assumption sufficient to capture the actual coupling mechanism between the thermal and concentration gradients.
is the partition function of the reactant state. A major concern in our simulation was whether or not the local rate constants could be considered a function of the local temperature, and if so is this assumption sufficient to capture the actual coupling mechanism between the thermal and concentration gradients.
Figure 2:
The simulation lattice above displays the imposed perodic boundrary conditions, vacancy locations, atom species, and the temperature field.
|
|
As shown in figure(2), our 2D simulation lattice is subject to periodic boundary conditions and a linear temperature gradient in the x direction. The transitions or diffusive jumps are limited to only movements between the vacancy site and nearest neighbor atoms. Also, the temperature 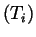 in the rate constant equation(5) is a function of the local lattice temperture (vacancy position). For example, given that the temperature in the positive x direction is decreasing,
in the rate constant equation(5) is a function of the local lattice temperture (vacancy position). For example, given that the temperature in the positive x direction is decreasing, 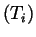 in equation(5) would be less for transitions to the right than for transitions to the left.
in equation(5) would be less for transitions to the right than for transitions to the left.



Next: Driven KMC Algorithm
Up: Methods
Previous: Methods
Shawn A. Putnam
2001-12-17
![\includegraphics[height=.15\textheight, width=.5\textwidth]{surface.bmp}](img13.gif)
![\includegraphics[height=.15\textheight, width=.5\textwidth]{surface.bmp}](img13.gif)
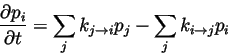
![\includegraphics[height=.35\textheight, width=.75\textwidth]{Lattice.bmp}](img24.gif)