Gear predictor-corrector algorithm

The existing code provided an implementation of the sixth order Gear predictor-corrector algorithm. The Berendsen thermostat and pressure control modulate the evolution of the system by scaling the velocities.

Defining scaled time derivatives of $\mathbf{r} = \mathbf{r}_0$ as $\mathbf{r}_1 = \delta t(\mathrm{d}\mathbf{r}_0/\mathrm{d}t)$, $\mathbf{r}_2 = \frac{1}{2}\delta t^2(\mathrm{d}^2\mathbf{r}_0/\mathrm{d}t^2)$, $\mathbf{r}_3 = \frac{1}{6}\delta t^3(\mathrm{d}^3\mathbf{r}_0/\mathrm{d}t^3)$, etc., the predictor step for a fourth order Gear algorithm can be written in matrix form [1]

$$\left( \begin{array}{c} \mathbf{r}_0^p(t+\delta t)\\ \mathbf... ...(t)\\ \mathbf{r}_2(t)\\ \mathbf{r}_3(t) \end{array} \right)\;.$$

The matrix is the Pascal triangle matrix and the generalization to the sixth order form is evident. The equations of motion enter through the corrector step. Evaluating the forces with $\mathbf{r}_0^p(t + \delta t)$ gives the correct second order derivative $\mathbf{r}_2^c(t+\delta t)$. The error in the prediction step is given by

$$\Delta\mathbf{r}_2(t+\delta t) = \mathbf{r}_2^c(t+\delta t) - \mathbf{r}_2^p(t+\delta t)\; .$$

Using this error the corrected values are

$$\left( \begin{array}{c} \mathbf{r}_0^c(t+\delta t)\\ \mathbf... ... \\ c_3 \end{array} \right) \Delta\mathbf{r}_2(t+\delta t)\; .$$

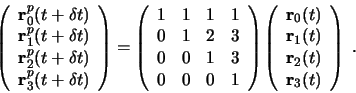
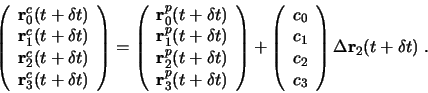
Gear discussed the best choice for the corrector coefficients $c_i$, which depends on how many derivatives of $\mathbf{r}_i$ are used [1,8,9]. The predictor-corrector algorithm has advantages over the Verlet algorithm only for small timesteps, but having the velocities available is convenient for implementing the Berendsen controls.