Verlet algorithm

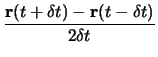The Nose-Hoover temperature and pressure controls are incorporated in the equations of motion as friction coefficients in the time integration which is performed using the Verlet algorithm [1],[17].

$$\mathbf{r}(t+\delta t) = 2 \mathbf{r}(t) - \mathbf{r}(t-\delta t) + \delta t^2 \mathbf{a}(t)$$ (4)

$$\mathbf{v}(t) = \frac{\mathbf{r}(t+\delta t) - \mathbf{r}(t-\delta t)}{2\delta t}$$

The first step of the integration was computed with ordinary Taylor expansion:

$$\mathbf{r}(t+\delta t) = \mathbf{r}(t) + \delta t \mathbf(v)(t) + \frac{1}{2} \delta t^2 \mathbf{a}(t)$$