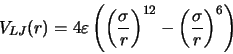
The Lennard-Jones potential

The Lennard-Jones pair potential is given by

$$V_{LJ}(r) = 4 \varepsilon\left(\left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6}\right)$$

where $r$ denotes the separation between the interacting particles. $\sigma$ is determined by the equilibrium distance, i.e. the situation of minimum energy. It sets the length scale for this kind of interaction. $\varepsilon$ is the depth of the potential and determines the energy scale.

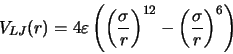
Lennard-Jones type interactions are assumed for Ar-Ar and Ar-Cu. The parameters are for Ar $\sigma_{\mbox{\footnotesize Ar-Ar}}=3.41$ Å, $\varepsilon_{\mbox{\footnotesize Ar-Ar}}/k_B=119.8$ K [1] (Maitland, 1981) and for Cu $\sigma_{\mbox{\footnotesize Cu-Cu}}=2.27$ Å, $\varepsilon_{\mbox{\footnotesize Cu-Cu}}/k_B=6765.4$ K (cf. homework #2). From the mixing rules of Lorentz and Berthelot [1] one approximates the values for Ar-Cu: $\sigma_{\mbox{Ar-Cu}}=2.84$ Å, $\varepsilon{\mbox{Ar-Cu}}/k_B=900.3$ K.

The potentials were evaluated numerically. In the code the energies and forces were calculated using spline interpolation.