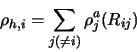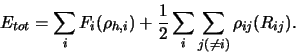
The more complex Cu-Cu interaction was computed in accord with the embedded atom method (EAM) [4], [5], [6].
In this approach the overall electron density in a metal is assumed
to be a linear-superposition of the contribution of each atom.
It is mainly affected by the contribution of the atom of reference whence
one approximates the other atoms by a constant term. The total
energy can then be written as
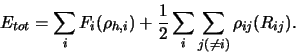
The electronic density ![]() is computed from the atomic
densities
is computed from the atomic
densities
![]() as follows:
as follows: