Theory

As outlined previously there is a considerable interest in methods to sample the canonical distribution with MD simulations and various techniques have been invented.

In the case of the canonical ($N$,$V$,$T$) ensemble the instantaneous kinetic energy is the conserved quantity in place of the total energy in the case of the microcanonical ($N$,$V$,$E$) ensemble. The most simple method to realize this situation in a simulation is by scaling the velocities. But one cannot expect to sample thereby the canonical ensemble. The same is true for two other techniques, the first one [2] employs random forces, the second one [3] is a more subtle way to scale the velocities. The scaling factor $\chi$ of the Berendsen thermostat is given by [1]

$$\chi = \left( 1 + \frac{\delta t}{\tau} \left(\frac{T}{\mathcal{T}}-1\right)\right)^{1/2}.$$

Here $T$ is the desired temperature, $\mathcal{T}$ the instantaneous kinetic temperature, $\delta t$ the time step and $\tau$ represents a rate which determines the coupling to the system.

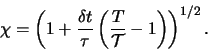
Nosé was the first to come up with a proper modification of the equations of motion so that they reproduce the canonical ensemble [13]. He introduces another degree of freedom $s$ which acts as a scaling factor for the velocities (or the time step, equivalently). Due to the parameter additional terms associated with its potential and kinetic energy appear in the Lagrangian and Hamiltonian, respectively. The conserved quantities in this system are the Hamiltonian, the total momentum and the total angular momentum. The equations of motion as derived from the Hamiltonian

$$\mathcal{H}_{\mbox{\footnotesize Nos\'e}} = \sum_i \frac{\... ... + \phi(\mathbf{r}) + \frac{p_s^2}{2 Q} + (f+1) k T_{eq} \ln s$$

are

$$\mathbf{\ddot{r}}_i = -\frac{\mathbf{F}_i}{m_i s^2}- \frac{2\dot s}{s}\mathbf{r}_i$$

$$Q\ddot s = \sum_i m_i s \mathbf{\ddot r}_i^2 - \frac{(f+1) k T_{eq}}{s}$$

where $\mathbf{p}_i$ are the momenta of the particles, $\mathbf{r}_i$ their positions and $\mathbf{F}_i$ the forces acting on them. $f$ stands for the number of degree of freedom of the unbiased system, $p_s$ is the conjugated momentum of $s$ and the parameter $Q$ determines the coupling of the system to the heat bath: the smaller it is the stronger the coupling. These equations are smooth, deterministic and on the contrary to the prementioned methods time-reversible. In fact, this approach represents a microcanonical ensemble with an additional coordinate. Using Liouville's theorem it can be shown that it is equivalent to a canonical ensemble with $f$ degrees of freedom.

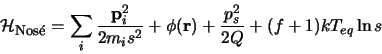
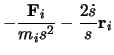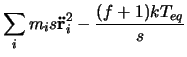Nosé's equations were reformulated [11] avoiding the scaling of the time step by introducing a new timestep containing $s$. Furthermore Hoover defined a friction coefficient $\xi\equiv p_s/Q$. The equations of motion become

$$\left. \begin{array}{rcl} \mathbf{\ddot r}_i & = & \frac{... ...thbf{p}_i^2/m_i - (f+1) k T_{eq}\right) \end{array} \right\}$$ (1)

Posch showed the effectiveness of the Nosé thermostat in sampling phase space for the classical one-dimensional harmonic oscillator [16]. Plotting $p$ versus $q$ for the microcanonical ensemble a perfect circle is obtained. Andersen´s method generates a number of points scattered over a circle. The Nosé-Hoover thermostat gives a broadened circle as expected if one allows fluctuations in the total energy (noting that the phase space volume corresponds to energy).