Implementation

In order to solve the eqs.(1) computationally they have to be discretized. Resolving the finite difference equations allows their implementation into the code. Holian gave explicit formulations for the Verlet algorithm [10] which translate to code as follows.

! x0,x1,x2 = positions and time derivatives in scaled units
real*8,dimension(3*NPMAX) :: x0,x1,x2
! f        = forces
real*8,dimension(3*NPMAX) :: f
! xi       = friction coefficient
real*8 :: xi
! trans    = kinetic energy in units of kB
real*8 :: trans
x2(i) = x2(i) - f(i)*x1(i)
x0(i) = two*x0(i) - x0old(i) + x2(i)
transavg = half*(trans+transold)
transold = trans
dK = two/(three*temp)*transavg - one
xi(i) = xi(i) + four*dK*deltat_fs/Q

In fig. 1 the temperature as a function of time as obtained in the MD simulation is shown. The cubic simulation box with side length 36.15Åcontained 2000 Cu atoms arranged on an fcc lattice. The initial velocities were set according to the Maxwell-Boltzmann distribution at temperature 600K.

Figure 1: The evolution of temperature with time for the Nosé-Hoover thermostat for different values of the coupling constant $Q$

Nosé has also given an expression for the period of oscillation depending on the choice of $Q$:

$$t_0 = 2 \pi \left( \frac{Q {\langle s\rangle}^2}{2 f k T_{eq}}\right)^{1/2}$$

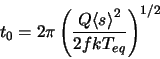
Another way to check if the thermostat operates correctly is to compute the heat capacity from the energy fluctuations

$${\langle\Delta E^2\rangle}_{NVT} = {\langle E^2\rangle}_{NVT} - {\langle E\rangle}_{NVT}^2 = k T^2 C_V$$

which can be rewritten in terms of the temperature and the fluctuations of the temperature

$$\langle\Delta T^2\rangle_{NVE} = T_{eq}^2 \frac{2}{3N} \left( 1 - \frac{3}{2 C_V} \right).$$