

Next: Local Energy
Up: Local Energy Calculation of
Previous: Local Energy Calculation of
This short paper summarizes the local energy calculation problem of the calculation of the Slater-Jastrow wave function. This wave function has number
of desirable properties for many-body quantum Monte-Carlo calculations
of electrons in the presence of ions.
The Slater-Jastrow wave function
is a product of Slater determinants and the Jastrow correlation factor:
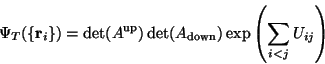 |
(1) |
Here, the
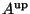 and
and
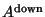 are defined as the
Slater matrices of the single particle up and down
orbitals, respectively. That is
are defined as the
Slater matrices of the single particle up and down
orbitals, respectively. That is
![\begin{displaymath}A = \left[
\begin{array}{ccccl}
\phi_1({\mathbf r}_1) & \phi...
...\vdots & \vdots & \vdots & \vdots & \ddots
\end{array}\right]
\end{displaymath}](img4.gif) |
(2) |
Where 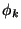 are molecular orbitals centered at
ck:
are molecular orbitals centered at
ck:
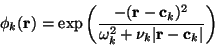 |
(3) |
The Jastrow correlation factor Uij terms are defined in the following manner:
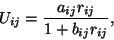 |
(4) |
where
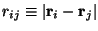 and
and
 |
|
|
(5) |
This trial wave function (1) has a number of desirable
properties:
- 1.
- The corerct cusp conditions for both like and unlike electron
spins.
- 2.
- The coorect cusp behavior as the electron-nuclear separation
becomes small.
- 3.
- The variational parameters in (1) have a simple
physical interpretation at large separations.
- (a)
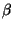 can be related to the polarizability of a molecule
can be related to the polarizability of a molecule
- (b)
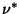 the maximum value of
the maximum value of 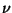 is equal to
is equal to
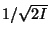 where I is the first ionization potential.
where I is the first ionization potential.


Next: Local Energy
Up: Local Energy Calculation of
Previous: Local Energy Calculation of
Nichols A. Romero
1999-12-17
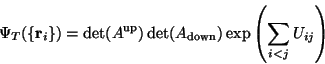
![\begin{displaymath}A = \left[
\begin{array}{ccccl}
\phi_1({\mathbf r}_1) & \phi...
...\vdots & \vdots & \vdots & \vdots & \ddots
\end{array}\right]
\end{displaymath}](img4.gif)
