

Next: Jastro correlation factor
Up: Local Energy Calculation of
Previous: Slater-Jastrow wave function
We wish to compute the local energy of the wave function, defined by
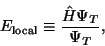 |
(6) |
where
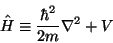 |
(7) |
The calculation of the potential energy V is straightforward. Therefore, we
will focus here the application of the Laplacian operator to the
Jastrow wave function. Given the form of the trial wave function, it
will prove convenient to define
We now attempt to calculation the action of 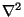 on
on 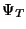 in
terms of
in
terms of
 .
.
This leaves a particularly simple form for the local energy.
![\begin{displaymath}E_{\text{local}}({\mathbf R}) = \frac{- \hbar^2}{2m} \left[ \...
... \nabla {\mathcal L}_T({\mathbf R}))^2\right] + V({\mathbf R})
\end{displaymath}](img28.gif) |
(10) |
Now, we are left with the task of computing
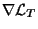 and
and
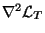 .
.
The gradient and Laplacian are linear operators, using
(8), we can find action of these operators on each of
the terms in the sum.


Next: Jastro correlation factor
Up: Local Energy Calculation of
Previous: Slater-Jastrow wave function
Nichols A. Romero
1999-12-17
![]() on
on ![]() in
terms of
in
terms of
![]() .
.