 |
The other choice to be made is the representation of the clusters. Earlier studies have employed internal coordinates (inter-atomic distances), where as some of the recent studies have employed space-fixed cartesian coordinates [1,8,9,10]. The space-fixed coordinates require 3n variables, whereas the internal-coordinates have n(n-1)/2 variables. Therefore, the space-fixed coordinates are more compact (require less variables) than the internal-coordinate representation for clusters with more than 6 atoms. Even though there can be infinitely many optimal structures in space-fixed coordinates (due to translation, and rotation), all the studies have shown that space-fixed representation is better than the internal-coordinate representation in terms of the algorithm efficiency. In the present study each atom is represented by cartesian coordinates (x,y,z) . Each coordinate is represented by a 5 bit binary string. For eg., a 4 atom cluster is fully represented by a 60 bit string length.
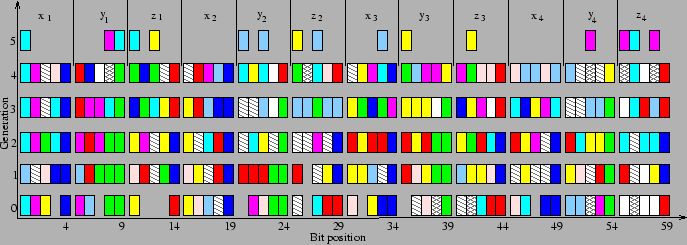
Niesse and Mayne [1] state that ``the representation in space-fixed coordinates is plainly contradictory to the spirit of Goldberg's ``building block(BB) hypothesis''; none of the coordinates stand alone as a meaningful BB.''. This observation is incorrect, a BB need not be meaningful in the physical sense. A particular allele or set of alleles (of lower order) that have significant effect on the fitness of individuals form a BB. It might happen that in a given population some genes are highly correlated and hence form a BB. This claim is illustrated in fig. 2, where the BBs are as identified by ECGA for the case of 4 atom Si cluster. As can be seen in the figure in the initial generation the higher order bits of each coordinate form BBs and in the later generations the lower order bits form BBs. This clearly indicates the domino convergence effect [30]. This also shows that any crossover operator that does not respect the BBs result in poor performance. This is mostly the case with single point crossover.
 |