The MPM concept is illustrated as follows: consider 4 bit problem and chose the following partition [0,2], [1], [3]. This partition implies that 0
![]() and 2
and 2
![]() bit are jointly distributed and the 1
bit are jointly distributed and the 1
![]() and the 3
and the 3
![]() bits are independently distributed. Therefore [0,2] can take the following four values, 00, 01, 10, and 11. The probability distribution for this partition is simply the frequency of individuals with those bit values. Similarly [1] and [3] can take either 0 or 1 and the proportion of individuals have on 1 and 0 in the 1
bits are independently distributed. Therefore [0,2] can take the following four values, 00, 01, 10, and 11. The probability distribution for this partition is simply the frequency of individuals with those bit values. Similarly [1] and [3] can take either 0 or 1 and the proportion of individuals have on 1 and 0 in the 1
![]() (and similarly in the 3
(and similarly in the 3
![]() bit) is the probability distribution for that partition.
bit) is the probability distribution for that partition.
A flowchart of ECGA procedure is given in fig. 3. Two things need further explanation, one is the identification of MPM using MDL and the other is the creation of a new population based on MPM. The identification of MPM in every generation is formulated as a constrained optimization problem,
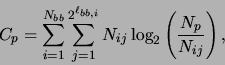 |
(8) |
A new population is generated based on the optimal MPM as follows, population of size ![]() where
where ![]() is the crossover probability, is filled by the best individuals in the current population. This differs from the original ECGA procedure [33] in which
is the crossover probability, is filled by the best individuals in the current population. This differs from the original ECGA procedure [33] in which ![]() individuals were taken to be the last
individuals were taken to be the last ![]() individuals of the current generation irrespective of their fitness. The rest
individuals of the current generation irrespective of their fitness. The rest ![]() individuals are generated by randomly choosing subsets from the current individuals. These subsets are the gene groups identified by the current MPM. This procedure is also different from the original ECGA procedure in which the subsets were chosen by probabilistic polling. The original procedure leads to a stochastic method were as the one used in the current study is a deterministic method in which the frequencies of the bit sequence of a particular subset remains constant. However, it has been observed that the outcome of both the methods are similar and in fact the deterministic method is computationally much faster.
individuals are generated by randomly choosing subsets from the current individuals. These subsets are the gene groups identified by the current MPM. This procedure is also different from the original ECGA procedure in which the subsets were chosen by probabilistic polling. The original procedure leads to a stochastic method were as the one used in the current study is a deterministic method in which the frequencies of the bit sequence of a particular subset remains constant. However, it has been observed that the outcome of both the methods are similar and in fact the deterministic method is computationally much faster.