


Next: Lattice Concentration Data
Up: Results and Discussion
Previous: Energy Barrier Calculations
We anticipated on solving for the self diffusion coefficient by applying the Einstein relation,
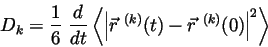 |
(10) |
where
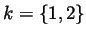 corresponding to
corresponding to 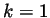 representing the Ar atoms, and
representing the Ar atoms, and 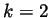 representing the Xe atoms. In theory, when a non-equilibrium steady state has been reached the diffusion flux will equal zero, and the self diffusion coefficient should approach a constant.
representing the Xe atoms. In theory, when a non-equilibrium steady state has been reached the diffusion flux will equal zero, and the self diffusion coefficient should approach a constant.
Figure 8:
Ar data of
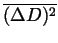 vs. time for different temperature gradients, where Grad=0.15
vs. time for different temperature gradients, where Grad=0.15
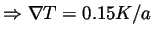 , and
, and
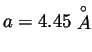 .
.
|
|
Figures(8,9) display data of the mean square displacement vs. time for several trials at varying temperature gradients. The data displayed was taken on a (250x100) Ar-Xe simulation lattice with an Ar concentration of 20 percent. In contradiction to experimental results, the self diffusion of Xe is greater than the self diffusion of Ar. In addition, the magnitude of the self diffusion coefficients differ from experiment. However, we attribute this to the value of the frequency factor 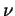 used in the simulation. Ideally we need to fit initial trials with
used in the simulation. Ideally we need to fit initial trials with 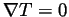 to experimental data. Thus, solving for
to experimental data. Thus, solving for 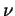 and then running the simulations with the fitted
and then running the simulations with the fitted 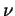 at varying temperature gradients.
at varying temperature gradients.
Figure 9:
Xe data of
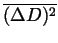 vs. time for different temperature gradients, where Grad=0.15
vs. time for different temperature gradients, where Grad=0.15
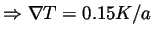 , and
, and
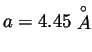 .
.
|
|



Next: Lattice Concentration Data
Up: Results and Discussion
Previous: Energy Barrier Calculations
Shawn A. Putnam
2001-12-17