Energy Barrier Calculations

Figure 5: Xe-Xe potential surface developed via Mathematica software. Nearest and next-nearest neighbor interactions where computed with a L-J potential where the yellow sphere represents a diffusing Xe atom.

We simulated the thermal diffusion of both Ar-Xe and Ar-Kr binary systems in 2 dimensions. The lattice was subject to a temperature gradient with a maximum temperature below the triple point. A Lennard-Jones potential was used in determining the potential energy surface or in general the energy barriers 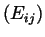$(E_{ij})$. Figure(1) depicts the a hypothetical potential energy surface in one dimension  [6], and figure(5) displays a plot for Xe-Xe diffusion in 3D. The L-J potential of two atoms at a separation R is given as:

$$U(R) = 4 \epsilon \left[\left(\frac{\sigma}{R}\right)^{12} - \left(\frac{\sigma}{R}\right)^{6} \right]$$ (7)

We assumed that the potential energy surface is independent of temperature such that the parameters 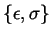$\left\{\epsilon,\sigma\right\}$ in the L-J potential between similar atoms can be taken from literature. With respect to the parameters 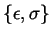$\left\{\epsilon,\sigma\right\}$ in the L-J potential between two different atoms, 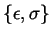$\left\{\epsilon,\sigma\right\}$ will be calculated with Lorentz-Berthelot mixing rules  [5] [2]. Corrections due to excess fluctuations are not considered such that the equations below apply.

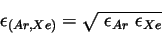$$\epsilon_{(Ar,Xe)} = \sqrt{\ \epsilon_{Ar} \ \epsilon_{Xe}}$$ (8)

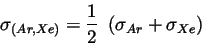$$\sigma_{(Ar,Xe)} = \frac{1}{2} \ \left(\sigma_{Ar} + \sigma_{Xe}\right)$$ (9)

Figures(6,7) display calculated barrier data for different lattice constants. The calculations were made for both a diffusing Ar and Xe atom surrounded by nearest and next-nearest Xe atoms (see figure(5)).

Figure 6: Energy barriers calculated via L-J using Xe nearest and next-nearest neighbors with a lattice constant equal to 4.45 $\stackrel{\circ}{A}$. The diffusing atom is Ar in the red plot and Xe in the black plot.

As shown by the plots, the lattice constant is the most influential parameter in the calculations. In determination of an approximate lattice constant, we generated a lattice of 2 species in proportion to their concentration distributed randomly. This was then used to determine the total energy of the lattice (LJ interactions) as a function of lattice constant by performing the lattice sums. This function was then minimized to get the approximate lattice constant.

Figure 7: A 2nd graph of the energy barriers calculated for Ar and Xe with a different lattice constant equal to 4.35 $\stackrel{\circ}{A}$.