Monte Carlo Simulation of Janus Rods and Comparison to Corresponding RISM Integral Equation Theory Results

Experimental

I. – Simulation Setup

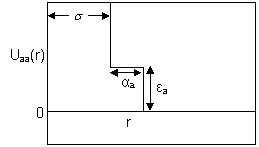
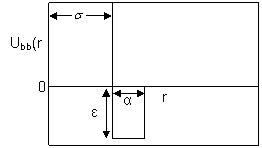
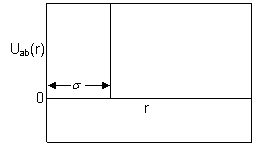
The rods are modeled as four site tangent bead model with two sites interacting via an attractive square well potential and the other two via a repulsive step potential. The potential profiles can be seen in figures 4-6 with σ as the hard core diameter, α as the potential range and Ɛ as the reduced potential depth.

Figure 3. - Four site rigid rod tangent bead model of a Janus Rod

Figure 4. – Potential interaction between two repulsive beads ^[1].

Figure 5. – Potential interaction between two attractive beads ^[1].

Figure 6. – Potential interaction between and attractive and repulsive bead ^[1].

II. – Monte Carlo Algorithm

1.) Rod Initialization - Initializing the rods was done in a layering fashion; one layer was completely filed up and then the next were done analogously until all rods were used up in an anti-parallel fashion to maximize the randomization; the initialization can be seen in figure 7. For lower density situations the rods were spaced accordingly to maximize spacing between rods in all directions.

Figure 7. – Rod initialization for a Janus rod packing fraction of 0.21.

2.) Rod Translation/Rotation – Rods were sequentially picked in a non-random order; and once the rods were chosen six possible moves could be performed. Five of the six possible moves correspond to a random rotation about any of the four beads or the center of mass. The sixth possible move was a random displacement in any direction. Translation and rotation moves were never combined so as to maximize the acceptance ratio.

3.) Acceptance/Rejection – After a single rod was moved, the new potential energy of the lone rod was calculated and the energy change computed. From the energy change, the move was accepted or rejected based off of the Metropolis Monte Carlo Scheme ^[2].

III. - Conditions

Throughout the simulations the number of tangent beads was kept the same as well as the aspect ratio (length/diameter). The aspect ratios of the rods were kept at 4.0 with hard core diameters of 1.0 (using reduced units). Parameters consisting of the potential depth, potential range, attractive repulsive potential ratio, and most importantly packing fraction were varied. While all parameters were varied only results on systems at a packing fraction of 0.21 and potential strengths of 5.4, 2.7, 1.35, and 0.7 with potential ranges of 0.10 and a potential ratio of 1.0 (as attractive as it is repulsive) are shown.

[1] Mukta Tripathy/Kenneth Schwiezer – Soft materials seminar presentation.

[2] Metropolis, N..; Rosenbluth, A. W.; Rosenbluth, M. N.; Teller, A. H. Equation of State Calculations by Fast Computing Machines J. Chem. Phys. 1953, 21, 1087-1092.

Introduction

Abstract

Results/Discussion

Conclusion

Acknowledgments