|
Results/Discussion |
|
The high
density case was the attempt at realizing microphase separation as predicted
using the RISM approach. As a gauge of equilibration we took energy traces of
every system. One representative example of a high density energy trace can
be seen as figure 8.
Figure
8. – Energy trace for a packing fraction of 0.21, energy of attraction and
repulsion of 5.4, ratio of 1.0, and an potential range of 0.1. From figure 8,
it is evident that that run looks fully equilibrated; but, ~70,000 runs is
not enough to say for certain and more runs are needed. Screenshots of
our system near the equilibration point are shown for various conditions as
figures 9 – 13.
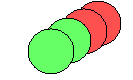
Figure
9. – System at a packing fraction of 0.21, attraction/repulsion energy of
5.4, ratio of 1.0, and an attractive range of 0.1.
Figure
10. - System at a packing fraction of 0.21, attraction/repulsion energy of
2.7, ratio of 2.0, and an attractive range of 0.1.
Figure
11. - System at a packing fraction of 0.21, attraction/repulsion energy of
2.7, ratio of 1.0, and an attractive range of 0.1.
Figure
12. - System at a packing fraction of 0.21, attraction/repulsion energy of
1.35, ratio of 1.0, and an attractive range of 0.01.
Figure
13. - System at a packing fraction of 0.21, attraction/repulsion energy of
0.7, ratio of 1.0, and an attractive range of 0.01. From figures
9-13 it is apparent that microphase separation may be setting in. For the
strongest attraction case shown in figure 10 it is evident that the rods
never fully break apart and disperse throughout the system like the systems
captured in figures 11-14. This supports that a large scale structure may be
forming which would need more particles to fully capture from simulation.
Figures 11-14 show that more of the box is explored and smaller
clumps/aggregates form in various regions of the box when the potential is
lower. Each of the
simulations has one characteristic feature common to all with this being the
end separation. Readily, one can see from all figures that greens aggregate
with greens and reds aggregate with reds. The reds, or repulsive, ends are
not really aggregating but apparently have no choice but to approach one
another in order for the greens, or attractive ends, to approach. From the
images it is hard to tell how close the reds are really relative to the
greens as the length of the attraction and repulsion is extremely small so a
large spacing is not necessary for energetic favoritism. From the
figures one can also see that there is some sort of local ordering of the
rods geometrically. One of two possibilities exists for the net ordering of
the rods along the z-axis with the first being: the system has not fully
equilibrated yet and the system is evolving very slowly from the initial
configuration. The second, more interesting, possibility is that a
combination of phase separation and some sort of local nematic ordering may
be occurring at these densities. Finally, in
figure 13a the g(r) for a packing fraction of 0.21, well length of 0.1, and a
well depth of 2.7 can be seen. Figure 13b shows the RISM results from prior
work by Mukta Tripathy and Kenneth Schweizer.
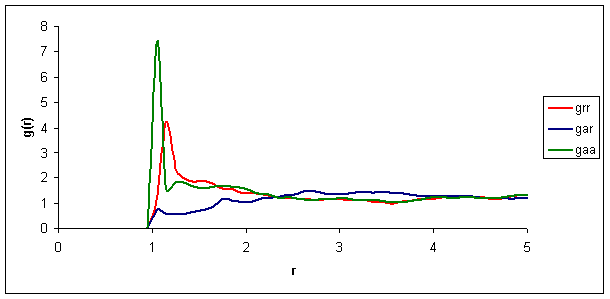
Figure 13a. –
Radial distribution functions obtained via simulation; however, not using
anti-parallel alignment and using significantly less runs (2,000 since the code
did not function for the long runs of 100,000 in printing g(r)).
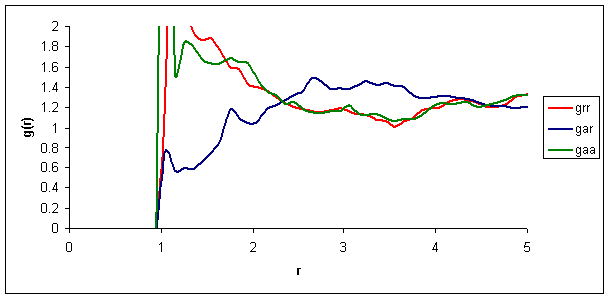
Figure 13b. –
Zoomed in radial distribution functions obtained via simulation; however, not
using anti-parallel alignment and using significantly less runs (2,000 since
the code did not function for the long runs on the Linux).
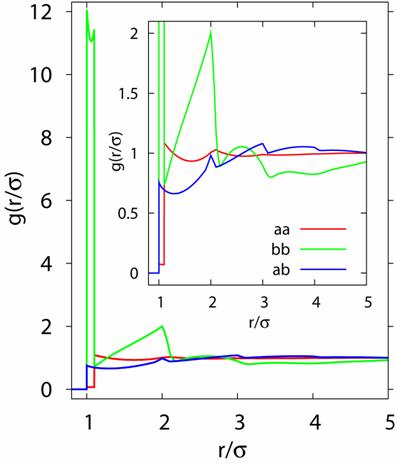
Figure
13c. – Results for the identical system in figures 13a and 13b using the RISM
integral equation approach [1]. From figures
13a thru 13c it is evident that very similar radial distribution functions
are obtained from both methods. Admittedly, the results in 13a and 13c were
obtained for a system which may be un-equilibrated; however, the similarities
are striking. The final
verdict on the actual microphase separated structures is still open; but, it
seems like parallel configurations of the rods with greens near greens and
reds near reds are preferable. The staggering of the rods so that the
repulsive ends face outwards does not seem to be the favored configuration
based off of these preliminary results. The staggered structure cannot be
ruled out until further simulations are done but even low density simulations
(next page) seem to favor the lined up arrangement of the rods. Go To: Low Density
Results [1] Mukta Tripathy/Kenneth Schwiezer – Soft
materials seminar presentation. |